آزمون دوجملهای

آزمون دوجملهای (Binomial) یک آزمون ناپارامتریک است که در آن بر مبنای یک مقدار یا مشخصه به بررسی موفقیت و شکست پرداخته میشود. منظور از موفقیت و شکست وجود یا عدم وجود یک متغیر در جامعه مورد بررسی میباشد.
یکی از آزمونهای پرکاربرد ناپارامتریمک آزمون دو جملهای یا آزمون نسبت موفقیت است. این آزمون معادل ناپارامتریک آزمون t تک نمونه است. اگرچه از آزمون علامت تک نمونه نیز میتوان به عنوان معادل ناپارامتریک آزمون t تک نمونه یاد کرد اما در SPSS تنها امکان استفاده از آزمون دو جملهای وجود دارد. آزمون دوجملهای binomial یک آزمون ناپارامتریک میباشد که در آن بر مبنای یک مقدار یا مشخصه به بررسی موفقیت و شکست پرداخته میشود.
برای نمونه پژوهشگری درصدد است میزان رضایت مشتریان یک بانک را با استفاده از این آزمون بسنجد. وی با دو حالت رضایتمندی (موفقیت) و عدم وجود رضایت (شکست) سر و کار دارد. بنابراین برای وجود و یا عدم وجود یک متغیر از آزمون دوجملهای سود برده میشود. از این آزمون از آنجایی که با یک متغیر سرو کار داریم برای آزمون فرضیههای توصیفی استفاده میشود. برای درک بهتر آزمون دوجملهای نخست باید با مفهوم توزیع برنولی و توزیع دوجملهای آشنا شد.
توزیع برنولی و توزیع دوجملهای
آزمایشهایی که دارای دو پیامد باشد و احتمال وقوع هر پیامد از آزمایشی به آزمایش دیگر ثابت باشد، به هر آزمایش یک آزمایش برنولی گویند. توزیع تعداد موفقیتها (۰ یا ۱) نیز توزیع برنولی گفته میشود. در آزمایش برنولی احتمال موفقیت را با p و احتمال شکست با q نشان داده میشود بطوریکه: p=1-q
- هر آزمایش باید دارای دو پیامد باشد.
- احتمال وقوع هر پیامد از آزمایشی به آزمایش دیگر ثابت باشد.
- آزمایشها مستقل از هم صورت گیرد.
نمونهگیری با جایگذاری از یک جامعه محدود و نمونهگیری بدون جایگذاری از یک نامحدود یک آزمایش برنولی است.
توزیع دوجملهای
در n آزمایش برنولی با احتمال موفقیت p اگر متغیر تصادفی x تعداد موفقیتها باشد، توزیع احتمال x توزیع دوجملهای نامیده میشود. بنابراین متغیر تصادفی x میتواند مقادیر ۰ تا n را اختیار کند.
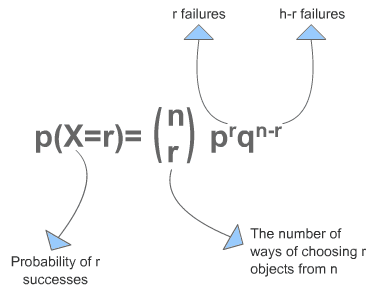
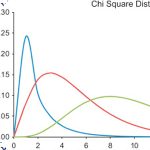
فرمول آزمون دوجمله ای
براساس قضیه حد مرکزی، شکل حدی توزیع دوجملهای، توزیع نرمال است. بطورکلی اگر np و nq هر دو از ۵ بزرگتر باشند، از توزیع نرمال به عنوان تقریبی برای توزیع دوجملهای استفاده میشود.
آزمون دو جملهای
آزمون دو جملهای معادل ناپارامتری آزمون t تک نمونهای میباشد، بدین معنا که اگر توزیع جامعه مشخص نباشد از آزمون دوجملهای به جای آزمون t تک نمونهای استفاده میگردد. از آزمون دو جملهای در SPSS زمانی استفاده میگردد که متغیری شامل دو مقدار باشد. از این آزمون زمانی استفاده میگردد که دو خصوصیات زیر برقرار باشد:
۱- هر یک از آزمایشات دو حالت داشته باشند. در واقع متغیرهای بولی Boolean که دارای دو حالت هستند در این نوع آزموت مورد استفاده قرار میگیرند مانند (موفقیت یا شکست)، (سالم یا خراب) و (درست یا نادرست) و … .
۲- تمامی مشاهدات باید از یکدیگر مستقل باشند یعنی پاسخ یک نمونه بر روی پاسخ نمونه دیگری تأثیرگذار نباشد.
آزمون دو جملهای در SPSS
از منوی Analyze وارد Nonparametric test و گزینه Binomial test را انتخاب کنید.
در پنجره باز شده یک یا چند متغیر را انتخاب کرده و به Test Variable List منتقل کنید.
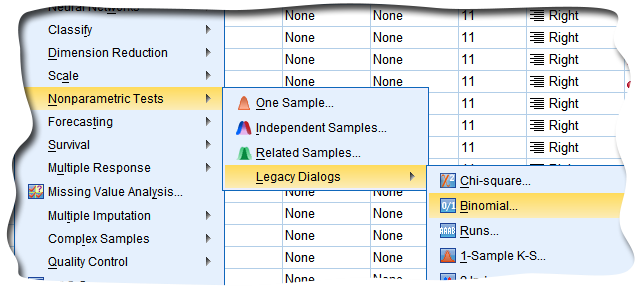
آزمون دو جملهای در SPSS
اگر این متغیرها دو حالتی هستند از گزینه Get From Data استفاده کنید و اگر دو حالتی نیستند و حالت کمی دارند و میخواهید آن را دو حالتی کنید گزینه Cut Point را انتخاب کنید و مقداری را در آن وارد کنید. مقادیری از دادهها که زیر نقطه Cut Point هستند، یک گروه تشکیل میدهند و مقادیری که بیشتر یا مساوی نقطه Cut Point میباشند، گروه دوم را تشکیل میدهند.
استفاده از آزمون دوجملهای در پرسشنامه با طیف لیکرت
می توان در متغیرهای کمی نیز از آزمون دوجملهای استفاده نمود به شرطی که یک نقطه را تعیین نمود و مقادیر را به دو گروه کمتر / بیشتر (از آن نقطه) تفکیک کرد. برای نمونه اگر میزان وفاداری مشتریان با طیف لیکرت ۵ درجه مورد سنجش قرار گرفته باشد نمره بالاتر از ۳ را به عنوان موفقیت و ۳ و کوچکتر از ۳ شکست در نظر گرفته میشود. این مسئله آزمون میشود که آیا نیمی از مشتریان وفاداری بالا دارند یا خیر (در نیمی از آنها موفقیت وجود دارد یا خیر).
فرضیه آزمون دوجملهای به صورت زیر میباشد:
قبل از انجام آزمون یک سطح خطا که معمولا ۵ صدم است در نظر گرفته میشود و دو فرضیه آماری زیر تدوین میشود
فرض صفر: درصد موفقیت در جامعه برابر نسبت آزمون است.
فرض مقابل : درصد موفقیت در جامعه برابر نسبت آزمون نیست.
با مشخص نمودن وضعیت شکست و موفقیت یک درصد احتمال برای هر یک از این دو وضعیت در نظر گرفته میشود و آزمون انجام میگیرد. چنانچه سطح معناداری کمتر از سطح خطای در نظر گرفته شده باشد فرض صفر رد شده و نتیجه میشود که درصد موفقیت و به تبع آن شکست برابر با حد ارایه شده در آزمون نیست. برای مشخص نمودن میزان نسبت به احتمال مشاهده شده توجه میشود.
جمعبندی
برای بررسی شانس موفقیت و شکست یک رویداد میتوان از آزمون دوجملهای استفاده کرد. از آنجا که این آزمون در زمره آزمونهای ناپارمتریک قرار داد بنابراین به توزیع جامعه وابسته نیست. این ویژگی سبب شده است تا از این آزمون به عنوان جایگزینی برای آزمون تی-تک نمونه وقتی دادهها نرمال نیست، استفاده شود. همچنین برای دادههای طیف لیکرت نیز میتوان از آزمون دوجملهای استفاده کرد.
منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). کتاب آموزش SPSS، تهران: انتشارات نارون.
آمار کاربردی مدیریت | ۱۵ خرداد ۹۸




سلام خسته خسته نباشید ببخشید من برای فصل سوم پایان نامه نیاز به فرمول محاسبه ی تی دو جمله ای دارم اگه امکانش هست کمکم کنید ممنونم از شما
آزمونی به نام تی دو جمله ای نداریم. اگر منظور شما تی-مستقل یا تی-زوجی است به بحث آزمونهای میانگین جامعه رجوع کنید. اگر منظور شما همین آزمون دو جملهای است که فرمول این آزمون هم در شکل بالای صفحه و هم درون متن آمده است.
سلام
آزمون دو جمله ای را میشه با اکسل هم انجام داد؟
از تابع زیر برای آزمون دو جملهای در اکسل استفاده میشود:
BINOM.DIST(number_s, trials, probability_s, cumulative)
ممنونم
چه داده هایی را باید داخل این تابع قرار بدم؟
منظور شما رو دقیق متوجه نمیشم. تا حد ممکن کوشش شد در این مطلب، آزمون دوجملهای را تشریح کنم.
سلام
برای پایان نامه ای که عنوانش تاثیر کرونا بر اقتصاد است آیا می شود از آزمون دوجمله ای استفاده کرد.
برای بررسی تاثیر بهتر است که از آزمونهای رگرسیون یا مدل ساختاری استفاده کنید.
سلام وخداقوت و ممنون از سایت خوبتون یک
از نظر آماری ،استفاده از آزمون دوجمله ای برای غربال کردن شاخص ها،درست بوده یا خیر؟
خیلی ممنون میشم بفرمایید
درود بر شما. ایده شما اشتباه نیست اما من تابحال ندیدم از این روش برای غربالگری استفاده بشه.
با سلام.درباره آزمون دو جمله ای برای پرسشنامه لیکرت،لطفا درباره نحوه وارد کردن داده ها در spss توضیح بدید.مث عدد ۳ رو نقطه مرکز مد نظر قرار میدیم.حالا برای اعداد ماقبل و مابعد ۳ تمام اعداد وارد میشه؟
پاراگراف آخر رو بخونی همین رو نوشته
درود بر شما. استفاده از آزمون دوجملهای در پرسشنامه با طیف لیکرت به صورت کامل تشریح شده است. دوباره این مطلب را بخوانید.
سلام. لطفا منبع را قید بفرمایید جهت ارجاع. تشکر فراوان
حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: انتشارات نارون. ص ۱۷۷
با سلام، در استفاده این آزمون درطیف لیکرت، تکلیف متغیرهایی که میانگین آنها بیشتر از ۳ ولی sig آنها بزرگتر از ۰.۰۵ هست چیست؟ برای بررسی وضعیت مطلوب باید به کدام موارد اتکا کنیم؟
درود بر شما. در این آزمون ملاک میانگین سازهها نیست با شمارش تعداد موفقیت و شکست سر و کار داریم.