آزمون‌های تعقیبی

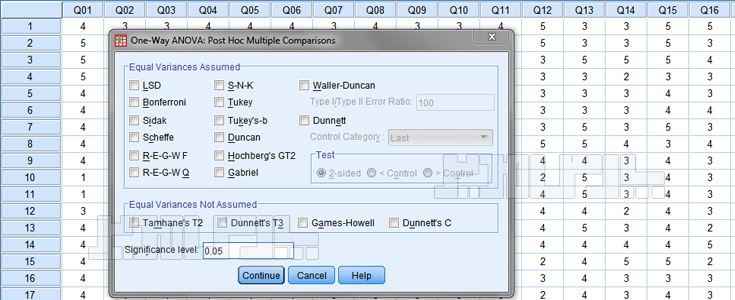
آزمون‌های تعقیبی (Post-hoc) روش‌های آماری هستند که برای تفسیر معناداری تفاوت میانگین طبقات در تحلیل واریانس استفاده می‌شوند. در واقع نتایج تحلیل واریانس نشان می‌دهد آیا اختلاف میانگین طبقات معنادار است یا خیر. اما این نتایج نشان نمی‌دهد کدام طبقات باهم تفاوت دارند. شماره زیادی از آزمون‌های تعقیبی وجود داند. برای نمونه می‌توان به آزمون توکی، شفه و تی دان اشاره کرد. در تحلیل واریانس برای مقایسه گروه‌ها در آزمون‌های تحلیل واریانس همچنین تحلیل واریانس نیز به شیوه‌های متعددی انجام می‌شود. تحلیل واریانس یک راهه، تحلیل واریانس چند راهه، تحلیل واریانس با اندازه‌های تکراری یک عاملی و جند عاملی، تحلیل واریانس چند متغیری و … از این جمله هستند.

پرسش کلیدی آن است که از چه آزمون تعقیبی استفاده شود که مناسب پژوهش مورد مطالعه باشد؟ پاسخ این پرسش اغلب برای پژوهشگران روشن نیست. پژوهشگران نمی دانند که با توجه به اهداف پژوهشی شان از چه آزمون تعقیبی برای مقایسه پش تجربی گروه‌ها استفاده کنند. در این مقاله بر آزمون‌های تعقیبی آمده است. این آموزش به پژوهشگران کمک کند تا آزمون تعقیبی مناسب را در تحلیل آماری پژوهش انتخاب کنند.

آشنایی با آزمون‌های تعقیبی

آزمون HSD و LSD مشهورترین آزمون‌های تعقیبی در تحلیل واربانس هستند. همچنین روش‌های گوناگون دیگری نیز برای بررسی اختلاف میانگین گروه‌ها در تحلیل واریانس وجود دارد که برخی از مهم‌ترین آنها عبارتند از:

آزمون توکی (HSD)

توکی (Tukey) به سال ۱۹۵۳ یک روش مقایسه چندگانه را بر مبنای آماره دامنه استیودنت پیشنهاد کرد. در روش وی از آزمون توکی، خروجی نرم‌افزار برای تعیین مقدار بحرانی تمام مقایسه‌های جفت میانگین‌ها استفاده می‌شود. بنابراین آزمون توکی در صورتی دو میانگین را دارای تفاوت معنی دار اعلام می‌کند که قدرمطلق اختلاف نمونه ی آن‌ها بیش از آزمون توکی، خروجی نرم‌افزار باشد. این آزمون که به HSD معروف است بعد از رد فرض صفر در آنالیز واریانس، به مقایسه ی همه ی تفاوت‌ها می‌پردازد. اگر در آزمون F تفاوت معناداری بین میانگین‌های گروهها ثابت شود، با آزمون توکی تفاوت معنادار مابین هر دو گروه بررسی می‌شود.

آزمون تفاوت معنادار راستین برگردان honestly significant difference است که به اختصار HSD نامیده می‌شود. این روش برای مقایسه دو به دو میانگین گروه‌ها استفاده می‌شود. آزمون توکی مقدار خطای کلی برای مجموعه مقایسه‌های دو به دو را کنترل می‌کند. این آزمون به طور متوسطی سخت گیر است و از طرفاغلب مولفان توصیه می‌شود.

آزمون توکی ب (Tukey s-b) حالت بیابینی از آزمون توکی و بونفرونی می‌باشد.

آزمون حداقل تفاوت معنی دار فیشر (LSD)

این آزمون یکی از قدیمی ترین و قوی ترین آزمون‌ها برای مقایسه پس از تجربه است. درصورتی که تعداد میانگین‌ها از سه تا بیشتر نباشد، بهتر است از این آزمون استفاده شود. اما اگر میانگین‌های مورد مقایسه بیش از سه مورد باشد، بهتر است سایر آزمون‌ها مورد استفاده قرار گیرد. آزمون حداقل تفاوت معنی دار (LSD) بسیار مشابه آزمون تفاوت معنی دار راستین (HSD) است.

آزمون حداقل تفاوت معنی دار (LSD) استفاده شده است که از روش مرسوم تفاوت معنادار راستین HSD روش سخت‌گیرانه‌تری است. دراین آزمون می‌خواهیم فرض H0:μi=μj را برای تمام i≠j آزمون نمائیم. چنانچه اختلاف میانگین بین دو گروه (تیمار) بیش از مقدار ثابت LSD باشد، به معنی اختلاف معنی دار بین دو گروه است. برای اجرای این آزمون توجه به دو نکته دارای اهمیت است؛ اول آنکه این آزمون بهتر است زمانی استفاده شود که مقدار آماره F در جدول آنالیز واریانس معنی دار شده باشد و دوم تعداد گروه‌ها زیاد نباشد.

آزمون حداقل تفاوت معنادار برگردان Least significant difference که به اختصار LSD نامیده می‌شود. این آزمون برای مقایسه دو به دو میانگین گروه‌ها به کار می‌رود. آزمون LSD خیلی ساده گیر (most liberal) است (یعنی توان بالایی دارد و احتمال زیادی دارد که مرتکب خطای نوع یک شود). بیشتر پژوهشگران در استفاده از این آزمون احتیاط می‌کنند، اما هنوز تمایل برای استفاده از این آزمون توسط برخی دیگر وجود دارد.

آزمون دانکن (Duncan)

در این آزمون، که به آزمون چند دامنه‌ای دانکن نیز معروف است، چنان چه قدر مطلق اختلاف میانگین‌های مورد مقایسه بزرگ تر یا مساوی rα(sx) باشد، اختلاف بین میانگین‌های مورد مقایسه معنی‌دار است. در این آزمون برای مقایسه هر جفت میانگین، مقدار rα(sx) خاص آن مقایسه محاسبه می‌شود.

بیشتر تصمیم‌گیری در مورد این که کدامیک از آزمون‌های معرفی شده ارجحیت دارد، کار دشواری است و بسته به نظر تحلیلگر آماری مربوطه دارد، لیکن کارمر و اسوانسن در مطالعه‌ای که در مورد تعدادی از روش‌های مقایسه‌ای چندگانه انجام دادند اعلام کردند که روش حداقل اختلاف معنی دار روش بسیار مؤثری برای نشان دادن اختلاف‌های واقعی میانگین‌ها می‌باشد. مشروط بر این که تنها پس از معنی دار بودن آزمون f تجزیه واریانس استفاده شود. آن‌ها همچنین قابلیت شناسایی مناسب تفاوت‌های واقعی را با استفاده از آزمون چند دامنه‌ای دانکن گزارش کردند.

آزمون دانکن برای مقایسه‌های دو به دو (مانند آزمون SNK، REGWF و REGWQ می‌باشد) به کار می‌رود. این آزمون به طور متوسطی ساده‌گیرانه است اما خطای نوع یک را در قالب آزمایش، و نه با تعدیل در مقایسه‌ها، کنترل می‌کند.

بعدها والر و دانکن این روش را توسعه دادند. آزمون والر-دانکن (Waller-Duncan)  به پژوهشگر این اجازه را می‌دهد تا نسبت خطاینوع یک بر خطای نوع دو را در مقایسه‌ها دخالت دهد.

آزمون دانت (Dunnett)

زمانی که در پژوهش یک گروه کنترل وجود دارد و هدف مقایسه گروه  هایآزمایشی با گروه کنترل است. از آزمون دانت برای مقایسه دو به دو میانگین گروه‌ها با گروه کنترل استفادهمی شود.اما زمانی که واریانس متغیر وابسته در گروه‌ها برابر نباشد (تجانس واریانس‌ها برقرار نباشد) از آزمون های تعقیبی زیر برای مقایسه‌ها بین گروهی استفاده می‌شود.

آزمون تامبن  Tambane’s-T2) T2) :  از این آزمون برای مقایسه‌های دو به دو استفاده می‌شود و آزمون سخت‌گیری است.

آزمون دانت تی-سه T3 (Dunnett s T3) و آزمون دانت سی (Dunnett s C) : این آزمون‌ها بر پایه توزیع t-student،مقایسه‌ها را انجام می‌دهند و آزمون‌های میانه روی هستند.

در نهایت روش گیمز-هول (Games-Howell) برای مقایسه‌های دو به دو به کار می‌رود و آزمون ساده‌گیری است.

آزمون شفه (Scheffe test)

این آزمون به پژوهشگر امکان می‌دهد تا تمام حالت‌های مختلف مقایسه یک به یک میانگین‌ها و همچنین تمام ترکیب‌های چندتایی مقایسه میانگین‌ها را انجام دهد .در آزمون شفه، برای کنترل میزان احتمال خطای نوع اول، معیار تصمیم‌گیری در مورد فرضیه صفر یعنی مقدار بحرانی جهت تشخیص معنی دار بودن افزایش می‌یابد.

آزمون شفه برای مقایسه دو به دو میانگین‌ها به کار می‌رود و خیلی سخت‌گیر (most conservative) است. یعنی توان آزمون پایین و احتمال کمی در ارتکاب به خطای نوع I دارد. روش شفه در زمانی که هدف سنجش فرضیات نظری نامعلوم باشد که نیاز به دقت است، پر کاربردترین آزمون تعقیبی خواهد بود.

آزمون نیومن-کولز (The Newman-Keuls test)

این آزمون برای مقایسه‌های دو به دو به کار می‌رود. آزمون نیومن کولز آزمون میانه روی است اما تمایل به متورم شدن خطای نوع I را دارد و از طرف برخی مولفان توصیه نمی شود. این آزمون پس از اینکه آزمون Anova فرض صفر را رد کند، مقایسه‌های جفتی میان گروهها را انجام می‌دهد. فرض کنید که گروه‌هایی داریم که در آنها m1 < m2 < m3 ممکن است که برخی از آزمونها مقایسه‌های جفتی را برای موارد زیر نیز انجام دهند: یعنی گروه اول و سوم خیلی با هم متفاوت نیستند اما در عوض گروه اول و دوم تفاوت معنا داری با هم دارند.

آزمون نیومن-کولز، دقیقا برای پرهیز از چنین اتفاقی طراحی شده است. بخوص وقتی که آزمون اعلام کند که mi و mj که (mi < mj) تفاوت معناداری با هم ندارند آن گاه هر جفت از میانگین‌های ml و mn که mi ml mn mj از روش نیومن کلز معنا دار نخواهند بود. نتیجه ی این آزمون به صورت یک سری از گروه‌های دوتایی خواهد بود که در هرکدام از آنها آن دسته از گروهها که میانگین هایشان بنا بر سطح معناداری α تفاوت معناداری از هم دارند، قرار گرفته اند.

دیگر آزمون‌های تعقیبی

آزمون بونفرونی (Bonferoni)

به این آزمون همچنین آزمون دان نیز گفته می‌شود. از این روش برای مقایسه دو به دو میانگین‌ها به کار می‌رود. این روش به طور متوسطی (moderately) سخت گیر است. اگرچه این آزمون اغلب در ادبیات پژوهشی به کار می‌رود اما روشی است که با افزایش تعداد مقایسه‌ها تمایل بزرگتر نشان دادن تفاوت‌ها دارد.

آزمون سیداک (Sidak)

به این آزمون گاهی اوقات نیز سیداک-بونفرونی گفته می‌شود. از این روش برای مقایسه‌های دو به دو به کار می‌رود و سخت گیر تر از آزمون بونفرونی است. این آزمون یک آزمون تعقیبی میانه روی (نه ساده گیر است و نه سخت گیر) است.

آزمون REGWF و REGWQ

این آزمون‌ها برای مقایسه‌های دو به دو به کار می‌روند. هر دو اینآزمون‌ها از طریق مولفانی که از آزمون نیومن کولز استفاده می‌کنند، پیشنهاد می‌شود.

آزمون هاکبرگز GT2 (Hochbergs GT2)

این روش شبیه آزمون توکی است، امابه صورت ویژه برای آزمایش هایی طراحی شده است که اندازه نمونه در گروه‌ها نا برابر باشد.

آزمون گابریل (Gabriel)

آزمون گابریل نسخه ی ساده گیرتر آزمون هاکبرگز-GT2 می‌باشد.

جمع‌بندی بحث آزمون‌های تعقیبی

آزمون  هایی که در بالا نام برده شدند برای مقایسه میانگین گروه‌ها به کار برده می‌شوند. یعنی زمانیکه بخواهیم چند گروه را از نظر یک متغیر مقایسه کنیم. به این نوع مقایسه ها، مقایسه‌های بین گروهیگفته می‌شود. اما زمانی که هدف مقایسه درون گروهی یک متغیر باشد یعنی بخواهیم چند آزمون تکراریکه از یک متغیر در یک گروه به دست آمده است را با هم مقایسه کنیم، دیگر نمی توان از این آزمون‌ها استفادهنمود. برای مقایسه میانگین‌های درون گروهی سه آزمون تعقیبی LSD، بونفرونی و سیداک تعدیل شده اند کهآن‌ها را اینگونه نام گذاری می‌کنند: LSD تعدیل یافته، بونفرونی تعدیل یافته و سیداک تعدیل یافته. این آزمون هایتعدیل یافته پایه‌ای شبیه به آزمون تعدیل نشده خودشان دارند.

منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: نارون.