آزمون سوبل (محاسبه آنلاین)

آزمون سوبل Sobel test روشی برای سنجش معناداری اثر متغیر میانجی در آمار است. این آزمون توسط مایکل سوبل مطرح شده است که از اساتید دانشگاه کلمبیا در آمریکا است. چنانچه مقدار آماره آزمون با ازمون سوبل از مقدار بحرانی ۱/۹۶ بیشتر باشد اثر میانجی معنادار است.

آماره آزمون در این روش با فرمول زیر محاسبه می‌شود:

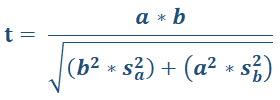
فرمول آزمون سوبل

در این رابطه:

• a: ضریب مسیر میان متغیر مستقل و میانجی
• b: ضریب مسیر میان متغیر میانجی و وابسته
• Sa: خطای استاندارد مسیر متغیر مستقل و میانجی
• Sb: خطای استاندارد مسیر متغیر میانجی و وابسته

آموزش محاسبه آنلاین آزمون سوبل

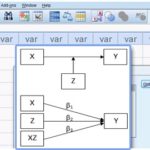
متغیر میانجی M به عنوان رابط بین متغیر مستقل و متغیر وابسته قرار می‌گیرد و به صورت جداگانه میزان رابطه متغیرهای مستقل و وابسته را تحت تاثیر قرار می‌دهد. یک مدل میانجی ساده در تصویر زیر نمایش داده شده است. نقش میانجی متغیر M از طریق ضریب اثر غیرمستقیم ab اندازه‌گیری می‌شود. هر چند می‌توان از راه بررسی معناداری ضرایب a و b به آزمون فرضیه میانجی پرداخت، امّا این روش توان آماری پایینی دارد. روش مناسب‌تر این است که به صورت مستقیم معناداری ضریب ab آزمون شود. یکی از پرکاربردترین روش‌ها برای این منظور آزمون سوبل (Sobel) است.

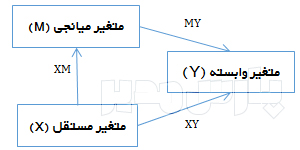
متغیر میانجی

ضریب بتای استاندارد متغیر مستقل و میانجی (a) را یادداشت کنید. برای تعیین خطای استاندارد در رگرسیون از جدول Model Summary قسمت Std. Error of the estimate استفاده کنید.

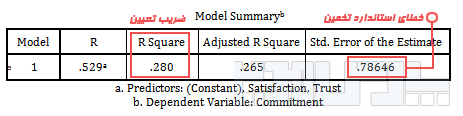
خطای استاندارد تخمین در رگرسیون

حال مدل رگرسیونی بین متغیر میانجی و وابسته را اجرا کنید. ضریب بتای استاندارد متغیر مستقل و میانجی (b) را یادداشت کنید. مانند گام پیش خطای استاندارد متغیرهای میانجی و وابسته (Sb) را نیز از یادداشت نمایید. مقادیر را در جای مناسب در فرمول بالای صفحه قرار دهید تا آزمون سوبل به صورت آنلاین محاسبه شود.

توسعه آزمون سوبل

آزمون سوبل رویکرد حاصل‌ضرب ضرایب، روش دلتا یا رویکرد نظریه نرمال هم نامیده شده است. آزمون سوبل برای انجام استنباط در مورد ضریب اثر غیرمستقیم ab، بر همان نظریه استنباط مورد استفاده برای اثر مستقیم مبتنی است. اثر غیرمستقیم ab یک برآورد خاص نمونه از اثر غیرمستقیم در جامعه (TaTb) است که در معرض واریانس نمونه‌گیری قرار دارد. با داشتن برآوردی از خطای استاندارد ab و با فرض نرمال بودن داده ها و توزیع نمونه‌گیری ab می‌توان یک p-value برای ab به دست آورد.

بطور کلی در آزمون سوبل می‌توان از تخمین نرمال برای بررسی معنی‌داری رابطه استفاده کرد. با داشتن برآورد خطای استاندارد اثر غیرمستقیم می‌توان فرضیه صفر را در مقابل فرض مخالف آزمون کرد. آماره Z برابر است با نسبت ab به خطای استاندارد آن. این فرمول توسط افراد دیگری مانند آروئیان و گودمن نیز توسعه داده شده است. فرمول برآورد معناداری نقش متغیر میانجی با روش پیشنهادی آروئیان به صورت زیر است:

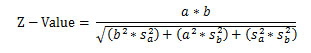
فرمول آزمون آروئیان

گودمن نیز فرمول مشابهی را ارائه کرده فقط به جای علامت مثبت در انتهای فرمول از علامت منفی استفاده کرده است.

تفسیر نتایج و جمع‌بندی

این برآوردگر حاصل‌ضرب مجذور خطاهای استاندارد را از دو عبارت اول معادله کم می‌کند. به دلیل این که در برآورد گودمن امکان منفی شدن خطای معیار وجود دارد استفاده از آن توصیه نمی شود. مقادیر a و b و خطاهای استاندارد آنها می‌توانند از خروجی تحلیل رگرسیون یا مدل معادلات ساختاری استخراج شوند. در نرم‌افزار SPSS برای به دست آوردن این مقادیر باید دو تحلیل رگرسیون اجرا شود:

اجرای یک تحلیل رگرسیون که در آن متغیر مستقل X متغیر پیش بین و متغیر میانجی M متغیر ملاک است. این تحلیل مقادیر a و sa رابه شما می‌دهد.

اجرای یک تحلیل رگرسیون که در آن متغیر مستقل X و متغیر میانجی M متغیر پیش بین و متغیر وابسته Y متغیر ملاک است. این تحلیل مقادیر b و sb رابه شما می‌دهد.

این محاسبات به سادگی می‌تواند با دست انجام شود. با در نظر گرفتن سطح خطای ∝=۰.۰۵ اگر مقدار Z از ۱/۹۶ بیشتر باشد، اثر غیرمستقیم مشاهده‌شده از نظر آماری معنادار است.

منبع: کتاب مدل‌یابی معادلات ساختاری نوشته آرش حبیبی و بهاره کلاهی