شمول واریانس (VAF) آمارهای است که میزان اثر میانجی یک متغیر در رابطه میان متغیر مستقل و متغیر وابسته را تعیین میکند. براساس مقدار این آماره مشخص میشود که اثر یک متغیر میانجی ضعیف، متوسط یا قوی برآورد شده است.
«شمول واریانس» برگردان variance accounted for است که به صورت اختصاری VAF نامیده میشود. در بررسی نقش میانجی متغیرها از این آماره نیز میتوان استفاده کرد هر چند باید با دست محاسبه شود. این روش در حداقل مربعات جزئی، رگرسیون، تحلیل مسیر و مدل معادلات ساختاری کاربرد دارد.
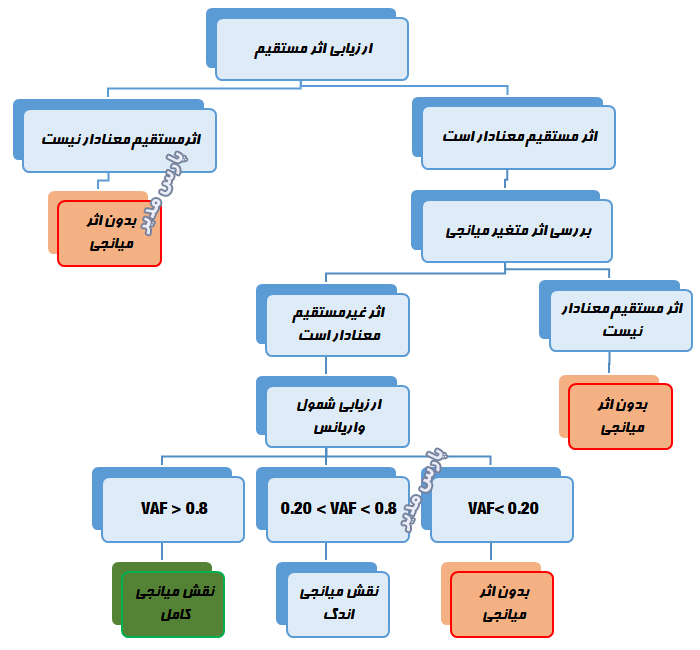
پیش از اجرای اثر میانجی باید مدل بدون متغیر میانجی اجرا شود. در این صورت باید اثر متغیر مستقل بر متغیر وابسته معنادار باشد. در غیر اینصورت بررسی نقش میانجی منتفی است. اگر اثر متغیر مستقل بر وابسته معنی دار بود مدل با حضور متغیر میانجی اجرا میشود. در این حالت باید تاثیر متغیر میانجی بر متغیر وابسته معنی دار باشد اگر چنین نباشد بازهم نقش میانجی منتفی است. در نهایت اگر همه شرایط برقرار باشد با استفاده از شمول واریانس میتوان به تفسیر نتایج پرداخت.
حالتهای متغیر میانجی (اقتباس از هیر و همکاران، ۲۰۱۳)
محاسبه آماره شمول واریانس VAF
شمول واریانس variance accounted for یا VAF نسبت اثر غیرمستقیم به کل اثر را نشان میدهد.
اثرمستقیم = اثر متغیر مستقل بر وابسته
اثر غیر مستقیم = اثر مستقل بر میانجی × اثر میانجی بر وابسته
اثر کل = اثر مستقیم + اثر غیر مستقیم
شمول واریانس = اثرغیرمستقیم ÷ اثر کل
جمعبندی و تفسیر نتایج
در نتیجه میتوان تعیین کرد که تا چه اندازه واریانس متغیر وابسته مستقیماً توسط متغیر مستقل تشریح میشود و چه مقدار واریانس هدف بوسیله روابط غیرمستقیم تشریح میشود. در نهایت نیز چه مقدار واریانس هدف بوسیله روابط غیرمستقیم از طریق متغیر میانجی شرح داده میشود.
اگر اثر غیرمستقیم معنادار باشد، اما هیچ اثری از متغیر پنهان مستقل بر متغیر درونزا را جذب نکند، شمول واریانس VAF نسبتاً پایین است. این زمانی روی میدهد که اثر مستقیم بالا باید و بعد از تحلیل متغیر میانجی با اثر غیرمستقیم معنادار، مقدار اندکی کاهش یابد. در این وضعیت، مقدار شمول واریانس VAF کمتر از ۲۰% خواهد بود و میتوان نتیجه گرفت که میانجیگری صورت نگرفته است. در مقابل وقتی مقدار VAF خیلی بزرگ و بالاتر از ۸۰% باشد، میتوان ادعای میانجیگری کامل کرد. وضعیتی که در آن VAF بین ۲۰% تا ۸۰% باید، به عنوان میانجیگری جزئی تشریح میشود.
منبع: حبیبی، آرش؛ جلالنیا، راحله. (۱۴۰۱). حداقل مربعات جزئی. تهران: نارون.