عدد فازی مثلثی (Triangular fuzzy number, TFN) یکی از انواع اعداد فازی است که با سه عدد حقیقی به صورت F=(l,m,u) نمایش داده میشود. این نوع از اعداد فازی به علت کارایی محاسباتی بسیار بالایی که دارند بسیار مرسوم هستند. بعلاوه محاسبات با این نوع از اعداد بسیار ساده و قابل فهم است. در این نوشتار، عدد فازی مثلثی مفهومسازی و تعریف خواهد شد.
آشنایی با عدد فازی مثلثی
منطق فازی با معرفی مجموعه فازی و سپس اعداد فازی کارایی پیدا کرد.
منطق فازی (Fuzzy Logic) رویکردی ریاضی و منطقی برای مدلسازی واقعیتهایی است که در آنها مرز بین درستی و نادرستی مطلق وجود ندارد. برخلاف منطق کلاسیک که هر گزاره یا درست (۱) یا نادرست (۰) است، در منطق فازی درجاتی از درستی تعریف میشود.
در دل این منطق، مفهوم عدد فازی (Fuzzy Number) شکل میگیرد؛ عددی که مقدار آن دقیق و قطعی نیست بلکه به صورت یک بازه یا مجموعهای از مقادیر با درجات عضویت بیان میشود. عدد فازی بهویژه در شرایطی کاربرد دارد که دادهها دقیق نیستند یا بر پایهی قضاوت انسانی استخراج شدهاند. این نوع عدد کمک میکند تا بتوان اطلاعات کیفی یا نادقیق را در محاسبات وارد کرد و به مدلهای واقعیتری دست یافت.
در میان انواع اعداد فازی، عدد فازی مثلثی (TFN) یکی از سادهترین و پرکاربردترین فرمهاست. این عدد با سه پارامتر مشخص میشود:
- مقدار کمینه (l)
- مقدار محتملترین یا مرکزی (m)
- مقدار بیشینه (u)
این ساختار ساده باعث میشود بتوان بهراحتی محاسبات فازی را انجام داد و دادههای نادقیق را بهشکل عددی مدلسازی کرد. به همین دلیل، عدد فازی مثلثی در بسیاری از روشها مانند فرایند تحلیل سلسلهمراتبی فازی یا در کتاب تصمیمگیری چندمعیاره فازی استفاده شود.
درجه عضویت فازی
برای درک بهتر این مفهوم، باید با مجموعه فازی و تابع عضویت آشنا شویم.
مجموعه فازی (Fuzzy Set) مجموعهای است که هر عنصر آن میتواند با درجهای بین صفر تا یک به آن تعلق داشته باشد، نه صرفاً تعلق کامل یا عدم تعلق مطلق. این درجه تعلق، توسط تابعی به نام تابع عضویت تعریف میشود.
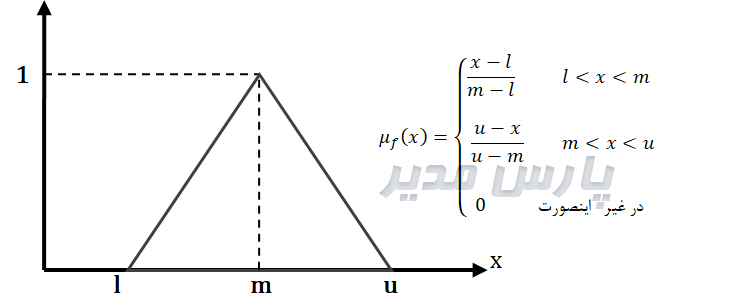
تابع عضویت (Membership Function) نشان میدهد که هر مقدار واقعی، تا چه حد به یک مفهوم یا دسته فازی تعلق دارد. در عدد فازی مثلثی، این تابع عضویت بهشکل یک مثلث است: از مقدار صفر (در کران پایین l) شروع میشود، در نقطه مرکزی (m) به حداکثر مقدار یعنی یک میرسد، و سپس در کران بالایی (u) دوباره به صفر بازمیگردد. درجه عضویت فازی یا تابع عضویت یک عدد فازی مثلثی به صورت زیر است:
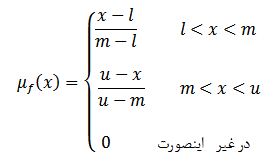
درجه عضویت یک عدد فازی مثلثی
عدد فازی مثلثی F=(l,m,u) در فضای هندسی به صورت زیر نمایش داده میشود.
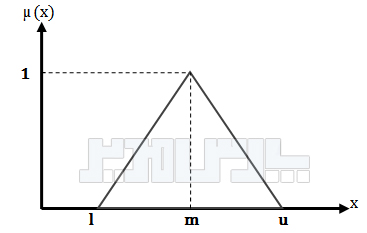
یک نمونه عدد فازی مثلثی
با توجه به تابع عضویت اعداد مثلثی مشخص است اگر x بین l و m باشد آنگاه هر چه بزرگتر باشد درجه عضویت آن نیز بزرگتر خواهد شد تا جائیکه برای x= m درجه عضویت برابر یک میشود. اگر x بین m و u باشد هرچه بزرگتر باشد، درجه عضویت کوچکتر خواهد شد و در x= u درجه عضویت صفر خواهد شد.
ساخت اعداد فازی مثلثی
عدد فازی مثلثی به دو نوع اصلی تقسیم میشود:
الف: عدد فازی مثلثی متقارن
در این حالت، فاصله بین مقدار مرکزی با کران بالا و پایین برابر است. یعنی:
m – l = u – m
مثال: عدد فازی مثلثی (۷۰, ۸۰, ۹۰)
در اینجا فاصله بین مقدار محتمل ۸۰ با کران بالا و پایین ۱۰ واحد است. این نوع زمانی مناسب است که عدم قطعیت بهطور مساوی در دو جهت وجود دارد.
شیوه ساخت: اگر عدد قطعی a و میزان عدم قطعیت δ باشد، عدد فازی مثلثی متقارن بهصورت (a−δ, a , a+δ) تعریف میشود.
ب: عدد فازی مثلثی نامتقارن
در این حالت، فاصله مقدار مرکزی با دو کران متفاوت است:
m – l ≠ u – m
مثال: عدد فازی مثلثی (۶۵, ۸۰, ۹۵)
اینجا فاصله تا کران پایین ۱۵ و تا کران بالا نیز ۱۵ است؛ اما اگر عددی مانند (۷۰, ۸۰, ۹۵) داشته باشیم، فاصلهها نامتقارن هستند (۱۰ و ۱۵).
نحوه ساخت: در شرایطی که داده یا ارزیابی ذهنی نشان دهد عدم قطعیت در یک سمت بیشتر است (مثلاً خوشبینانه یا بدبینانه)، مقدار مناسب برای هر کران انتخاب میشود.
استفاده از عدد فازی مثلثی متقارن یا نامتقارن بستگی به نوع داده، قضاوت خبرگان، یا نوسانات واقعی متغیر دارد. انتخاب درست نوع عدد فازی، دقت و واقعگرایی تحلیل را به شکل قابل توجهی افزایش میدهد.
عملیات جبری روی اعداد فازی مثلثی
کارایی محاسباتی اعداد فازی مثلثی به علت سادگی انجام عملیات ریاضی روی آن بسیار زیاد است. عملیات ریاضی روی اعداد فازی مانند F1 و F2 به صورت به سادگی قابل انجام است:

عملیات جبری روی اعداد فازی مثلثی
سخن پایانی
عدد فازی مثلثی یکی از انواع اعداد فازی است که کارایی محاسباتی بالایی دارد. در عین حال انجام محاسبات با این روش بسیار ساده است. با این وجود انواع دیگری از اعداد فازی نیز وجود دارند. برای نمونه میتوان به عدد فازی ذوزنقهای Trapezoidal اشاره کرد. اعداد ذوزنقهای به صورت F=(l,m1,m2,u) نمایش داده میشود.
به طور کلی در یک سیستم فازی نخست مقادیر کیفی باید به صورت اعداد فازی ذخیره شوند. به این عملیات فازیسازی گفته میشود. پس از آن استنتاج فازی صورت میگیرد. زمانیکه عملیات فازی بر روی مقادیر انجام شد در نهایت به نتایجی خواهید رسید که فازی هستند. این نتایج فازی بسادگی قابل فهم و تفسیر نیستند بنابراین باید به اعداد قطعی (معمولی) تبدیل شوند. فرایند تبدیل اعداد فازی مثلثی به اعداد قطعی را فازیزدایی گویند.
منبع: حبیبی، آرش؛ آفریدی، صنم. (۱۴۰۱). تصمیمگیری چندشاخصه. تهران: ناروندانش.
سوالات متداول
عدد فازی مثلثی سه نقطه (l, m, u) دارد و تابع عضیت آن یک قله دارد. اما عدد فازی ذوزنقهای با چهار نقطه (a, b, c, d) تعریف میشود و بین b و c مقدار عضویت برابر ۱ است؛ یعنی اوج عضویت گستردهتری دارد.
میزان عدم قطعیت معمولاً بر اساس یکی از این روشها تعیین میشود: تحلیل آماری (مثل انحراف معیار یا دامنه تغییرات)، قضاوت خبرگان، استفاده از مقیاسهای استاندارد در مطالعات مشابه، یا بررسی نوسانات تجربی دادهها. انتخاب روش باید با ماهیت داده و هدف مدلسازی متناسب باشد.