آمار توصیفی

آمار توصیفی (Descriptive Statistics) شاخه‌ای از آمار کاربردی است که به خلاصه‌سازی، طبقه‌بندی و نمایش داده‌ها برای درک الگوهای موجود می‌پردازد. در جهانی که حجم عظیمی از داده‌ها تولید می‌شود، فهم و تحلیل این داده‌ها بدون استفاده از روش‌های مناسب عملاً امکان‌پذیر نیست. نظر به اهمیت موضوع در این نوشتار، «آمار توصیفی» مفهوم‌سازی و تعریف خواهد شد.

تعریف آمار توصیفی

آمار توصیفی یکی از بنیادی‌ترین بخش‌های علم آمار است و نقش آن فراهم‌کردن امکان شناخت وضعیت موجود از طریق داده‌های گردآوری‌شده است. این شاخه از آمار تلاش می‌کند داده‌های خام را به اطلاعات قابل‌فهم تبدیل کند تا پژوهشگر، مدیر یا تحلیل‌گر بتواند بر اساس آن تصمیم‌گیری اولیه داشته باشد.

در این حوزه، تمرکز بر روی توصیف، طبقه‌بندی و نمایش داده‌هاست و نه استنتاج درباره جامعه بزرگ‌تر؛ همین ویژگی آن را از آمار استنباطی متمایز می‌سازد.

آمار توصیفی (Descriptive statistics) تنظیم و طبقه‌بندی داده‌ها، نمایش ترسیمی، و محاسبه مقادیری از قبیل نما، میانگین، میانه و … می‌باشد. این حوزه آماری، حاکی از مشخصات یکایک اعضای جامعه مورد بحث است.

از دیدگاه نظری، آمار توصیفی به ابزارها و روش‌هایی مانند میانگین، میانه، مد، انحراف معیار، واریانس، دامنه تغییرات و شاخص‌های پراکندگی متکی است. این شاخص‌ها هر کدام ابعادی از رفتار داده را مشخص می‌کنند؛ برای مثال میانگین نشانگر مقدار مرکزی، انحراف معیار بیانگر میزان پراکندگی و نمودارها و جدول‌ها تصویر ذهنی روشن‌تری از اطلاعات فراهم می‌کنند.

کارکردهای آمار توصیفی

در یک نگاه جامع، آمار توصیفی به سه حوزه اصلی تقسیم می‌شود:

• خلاصه‌سازی داده‌ها با شاخص‌های عددی
• نمایش داده‌ها با نمودار و جدول
• تحلیل الگوهای اولیه.

این سه بخش به پژوهشگر کمک می‌کند قبل از ورود به تحلیل‌های استنباطی یا مدل‌سازی پیچیده، درک دقیقی از وضعیت داده‌ها به دست آورد. اهمیت این مرحله در آن است که بسیاری از تصمیم‌ها و تحلیل‌های پیشرفته بدون شناخت مقدماتی داده‌ها ممکن است به نتایج نادرست منتهی شوند.

اهمیت آمار توصیفی

آمار توصیفی نقش ضروری و اولیه‌ای در تمامی پژوهش‌ها و فرایندهای تصمیم‌گیری دارد، زیرا نخستین تصویری است که از داده‌ها ارائه می‌شود و پایه تحلیل‌های بعدی را شکل می‌دهد.

دلایل اهمیت آمار توصیفی:

• شناخت وضعیت موجود: کمک به فهم رفتار کلی داده‌ها
• کاهش پیچیدگی: تبدیل حجم زیاد داده‌ها به اطلاعات قابل‌درک
• کمک به تصمیم‌گیری اولیه: ارائه نتایج سریع و قابل‌اتکا
• پایه تحلیل‌های پیشرفته: شرط لازم برای استفاده از آمار استنباطی و مدل‌سازی

آمار توصیفی نه‌تنها در پژوهش‌های علمی، بلکه در مدیریت، بازاریابی، علوم پزشکی، علوم اجتماعی و حتی تحلیل رفتار کاربران در شبکه‌های اجتماعی کاربرد گسترده دارد. این اهمیت موجب می‌شود افراد در هر سطح علمی نیازمند آشنایی با روش‌های توصیفی باشند.

آمار توصیفی با کمک نرم‌افزار SPSS

محاسبات مربوط به انواع شاخص‌های آمار توصیفی را در منوی Analyze زیرمنوی Descritive Statistics خواهید یافت. فراوانی‌ها، شاخص‌های توصیفی، جداول متقاطع و انواع نسبت‌ها در این قسمت قابل دسترسی است.

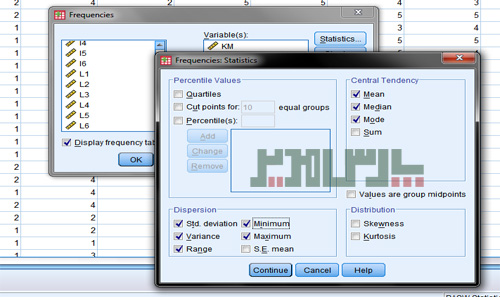
سه فرمان Frequencies, Descriptives و Crosstabs در کتاب SPSS پارس مدیر بررسی شده است. بطور کلی بخاطر داشته باشید برای بدست آوردن انواع فراوانی مراحل زیر را انجام دهید:

از منوی Analyze زیرمنوی Descritive Statistics و سپس Frequencies را انتخاب کنید.

متغیرهای مورد نظر را به کمک فلش به باکس Variables منتقل کنید.

دکمه Stattistics را بزنید تا کادر جدیدی باز شود.

میانگین، میانه، مد، انحراف معیار و هر آماره توصیف دلخواه دیگری که نیاز دارید را فعال کنید.

در پایان هر دو کادر را تایید کنید تا همه نوع خروجی توصیفی را در مشت داشته باشید.

 آموزش کامل آمار توصیفی

ابعاد مختلف آمار توصیفی هر یک بخشی از واقعیت داده‌ها را آشکار می‌کنند و در کنار هم تصویری کامل‌تر ارائه می‌دهند. ابعاد اصلی شامل موارد زیر است:

• شاخص‌های مرکزی: مانند میانگین، میانه، مد
• شاخص‌های پراکندگی: مثل انحراف معیار، واریانس، دامنه
• نمودارها و نمایش تصویری: نمودار میله‌ای، دایره‌ای، جعبه‌ای و خطی
• جدول‌ها و طبقه‌بندی: شامل جداول توزیع فراوانی

هر یک از این ابعاد برای تحلیل نوع خاصی از داده‌ها به کار می‌رود و ترکیب آن‌ها باعث می‌شود پژوهشگر فهم عمیق‌تری از الگوها و تغییرات داده به دست آورد. برای ورود به بحث آمار توصیفی ابتدا جامعه و نمونه تشریح شده است. سپس انواع متغیرهای پژوهش و انواع مقیاس اندازه‌گیری متغیرها بیان شده است.

جدول‌های فراوانی آماری

جدول فراوانی اولین گام برای تحلیل توصیفی و ترسیم نمودارهای آماری محسوب می‌شود. جدول فراوانی ابزاری است برای سازمان‌دهی داده‌ها و نشان دادن تعداد تکرار هر مقدار یا هر دسته.

• فراوانی
• فراوانی نسبی
• فراوانی تجمعی
• فراوانی نسبی تجمعی

اطلاعات بدست آمده از یک تحقیق غالباً توده‌ای از اطلاعات خام، بی معنی و بدون نظم هستند که هر نوع نتیجه‌گیری و تفسیر آنها غیر ممکن است. بنابراین برای هر نوع تجزیه و تحلیل اطلاعات لازم است داده‌ها براساس یک نظم منطقی طبقه بندی (Classification) شوند تا به صورت معنی‌دار و قابل تفسیر در آید.

• فراوانی: تعداد تکرار هر داده در مجموعه داده‌هاست و با fi​ نمایش داده می‌شود.
• فراوانی نسبی: نسبت فراوانی هر داده به کل داده‌هاست و سهم هر مقدار را در مجموعه نشان می‌دهد.
• فراوانی تجمعی: مجموع فراوانی یک دسته به‌همراه تمام دسته‌های قبلی است.

این جداول کمک می‌کنند توزیع داده‌ها به‌صورت ساختاریافته دیده شود و معمولاً شامل ستون‌های مقدار، فراوانی مطلق، فراوانی نسبی و فراوانی تجمعی است.

نمودارهای آماری

نمودارهای آماری نمایش تصویری داده‌ها هستند و فهم الگوها، روندها و توزیع داده را آسان می‌کنند. نمودارهایی مانند میله‌ای، دایره‌ای، خطی و هیستوگرام از رایج‌ترین انواع آن هستند. این نمودارها کمک می‌کنند تفاوت‌ها و تغییرات داده سریع‌تر و واضح‌تر دیده شود.

• هیستوگرام
• چندبر فراوانی
• چندبر فراوانی تجمعی
• منحنی‌های فراوانی
• نمودار شاخه و برگ

استفاده از نمودار باعث می‌شود تحلیل داده برای مخاطب غیرتخصصی هم قابل‌درک باشد. طبقه بندی داده‌ها تمام اطلاعات در یک جدول به نام جدول توزیع فراوانی (Frequeny Table) گردآوری می‌شود.

معیارهای مرکزی (Dispersion Index) 

معیارهای مرکزی نشان می‌دهند داده‌ها حول کدام مقدار متمرکز شده‌اند. میانگین، میانه و مد اصلی‌ترین شاخص‌های مرکزی هستند. این معیارها تصویری از «مقدار معمول» یا «نقطه مرکزی» داده ارائه می‌دهند. انتخاب شاخص مناسب به نوع داده و میزان پراکندگی آن بستگی دارد.

• میانگین
• میانه
• نما
• چندک ها

مد یا نما: در یک تعریف ساده، نما Mode به داده‌ای گفته می‌شود که در یک مجموعه از اعداد بیشتر از همه رخ دهد. برای مثال اگر در یک کلاس هفت نفر ۱۲ ساله باشند، ده نفر ۱۳ ساله باشند و چهار نفر ۱۴ ساله نما ۱۳ است زیرا بیش از هر سن دیگری ۱۳ ساله وجود دارد. در انتخابات به نما معمولا «حداکثر آرا» گفته می‌شود و نامزدی که بیشترین آرا را کسب کند برنده انتخابات است حتی اگر تعداد آرای او حداکثر (بیشتر از نصف) کل آرا نباشد.

میانه: میانه Median در وسط چند مقدار در یک مجموعه از مقدارها قرار دارد. برای مثال اگر سه دانش‌آموز در یک آزمون نمره‌های ۸۱، ۸۴ و ۹۳ گرفته باشند، مقدار وسط که ۸۴ است به عنوان میانه انتخاب می‌کنیم.

میانگین: میانگین Mean معمولی یا میانگین حسابی (که گاهی اوقات متوسط نیز نامیده می‌شود) برابر است با حاصل‌جمع تمام مقدارها تقسیم بر تعداد مقدارها. برای مثال اگر سه دانش‌آموز در یک آزمون نمره‌های ۸۱، ۸۴ و ۹۳ گرفته باشند، میانگین برابر است با ۸۱ + ۸۴ + ۹۳ / ۳ که می‌شود ۸۶.

معیارهای پراکندگی (Centrol Index)

معیارهای پراکندگی میزان پراکندگی یا فاصله داده‌ها از مقدار مرکزی را توصیف می‌کنند. شاخص‌هایی مانند دامنه تغییرات، واریانس و انحراف معیار در این دسته قرار می‌گیرند. این معیارها نشان می‌دهند داده‌ها چقدر از یکدیگر فاصله دارند و چقدر منسجم‌اند. تحلیل پراکندگی برای مقایسه چند مجموعه داده و ارزیابی نوسان‌ها ضروری است.

• دامنه
• میانگین انحرافها از میانگین
• میانگین انحرافها از میانه
• دامنه چارکی
• دامنه صدکی
• واریانس داده‌ها
• انحراف معیار
• ضریب تغییرات

انحراف معیار (Standard deviation) مفهومی است که میزان پراکندگی داده‌های یک مجموعه را مشخص می‌کند. بدین جهت یکی از مهم‌ترین مقیاس‌های آماری در زمینه آمار توصیفی به حساب می‌آید. اگر میانگین برآوردی از نقطه ثقل توزیع داده‌های یک مجموعه به دست می‌دهد. از این رو مقیاسی تک‌بعدی برای برآورد یک مجموعه داده‌ها فراهم می‌سازد. می‌توان گفت که انحراف معیار نیز میزان پراکندگی داده‌ها از نقطه میانگین را نشان می‌دهد. از این رو مقیاسی دوبعدی برای برآورد توزیع داده‌ها در اختیار ما قرار می‌دهد. واریانس به صورت «مقدار متوسط مربع اختلاف مقادیر از میانگین» تعریف شده است.

سخن پایانی

آمار توصیفی مرحله‌ای کلیدی در هر تحلیل علمی و پژوهشی است و به‌عنوان نخستین گام در فهم داده‌ها عمل می‌کند. این شاخه با ارائه شاخص‌های عددی و ابزارهای تصویری، امکان درک ساختار اولیه داده‌ها را فراهم می‌سازد و مسیر تحلیل‌های بعدی را هموار می‌کند. بدون شناخت توصیفی، ورود به تحلیل‌های استنباطی یا استفاده از مدل‌های پیچیده می‌تواند خطاهای جدی به دنبال داشته باشد. ازاین‌رو تسلط بر آمار توصیفی نه‌تنها برای پژوهشگران، بلکه برای مدیران و تحلیل‌گران داده نیز ضروری است. در پایان می‌توان گفت آمار توصیفی پایه و اساس تحلیل داده در تمام علوم است و نقش آن در تصمیم‌سازی دقیق و علمی، غیرقابل‌انکار است.

دانلود پاوپوینت آموزش آمار توصیفی

منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: نارون‌دانش.