چولگی و کشیدگی دادهها دو آزمون آماری برای ارزیابی میزان پراکندگی فراوانی دادهها بوده و برای بررسی نرمال بودن توزیع استفاده میشوند.
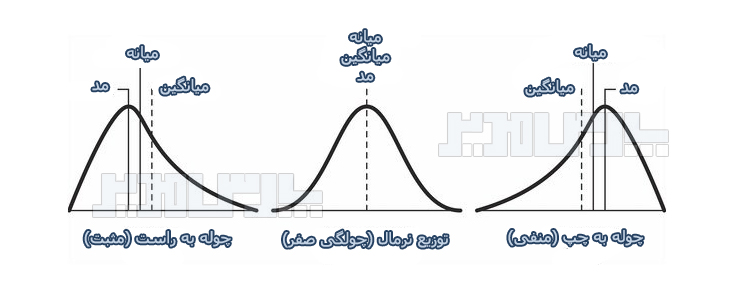
در علم آمار چولگی یا Skewness معیاری از تقارن یا عدم تقارن تابع توزیع میباشد. برای یک توزیع کاملاً متقارن چولگی صفر و برای یک توزیع نامتقارن با کشیدگی به سمت مقادیر بالاتر چولگی مثبت و برای توزیع نامتقارن با کشیدگی به سمت مقادیر کوچکتر مقدار چولگی منفی است.
کشیدگی یا Kurtosis نشان دهنده ارتفاع یک توزیع است. به عبارت دیگر کشیدگی معیاری از بلندی منحنی در نقطه ماکزیمم است و مقدار کشیدگی برای توزیع نرمال برابر ۳ میباشد. کشیدگی مثبت یعنی قله توزیع مورد نظر از توزیع نرمال بالاتر و کشیدگی منفی نشانه پایین تر بودن قله از توزیع نرمال است. برای مثال در توزیع t که پراکندگی دادهها بیشتر از توزیع نرمال است، ارتفاع منحنی کوتاه تر از منحنی نرمال است. از چولگی و کشیدگی برای آزمون نرمال بودن داده ها استفاده میشود.
کشیدگی دادهها
کشیدگی توزیع دادهها به عبارت ساده به همان ارتفاع توزیع دادهها اشاره میکند.
- مقدار کشیدگی برای توزیع نرمال برابر ۳ میباشد.
- کشیدگی مثبت یعنی قله توزیع مورد نظر از توزیع نرمال بالاتر است.
- کشیدگی منفی نشانه پایینتر بودن قله از توزیع نرمال است.
براساس یک تعریف علمی کشیدگی برابر با گشتاور چهارم نرمال شدهاست. کشیدگی معیاری از تیزی منحنی در نقطه ماکزیمم است. در آمار کشیدگی توصیف کننده میزان قلهای بودن و مسطح بودن یک توزیع احتمالی است. هرچقدر شکل تابع چگالی احتمال (probability density function) قلهای تر و دارای دم پهن تر یا دنباله پهن تر(fat-tailed/ heavy-tailed) باشد میزان شاخص کشیدگی برای آن بیشتر است.
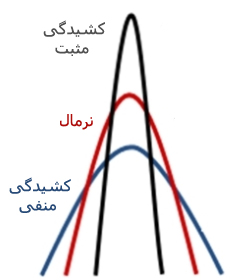
کشیدگی توزیع داده ها
چولگی داده ها
چولگی (Skewness) در آمار نشان دهنده میزان عدم تقارن توزیع احتمالی است. اگر دادهها نسبت به میانگین متقارن باشند، چولگی برابر صفر خواهد بود.
- چولگی یک توزیع کاملاً متقارن برابر صفر است.
- یک توزیع نامتقارن با کشیدگی به سمت مقادیر بالاتر، چولگی مثبت دارد.
- یک توزیع نامتقارن با کشیدگی به سمت مقادیر کوچکتر، چولگی منفی دارد.
در خروجی آزمون چولگی و کشیدگی دادهها با SPSS میزان خطای استاندارد نیز قابل مشاهده است. برای بررسی نرمال بودن دادهها باید «نسبت چولگی» و «نسبت کشیدگی» را حساب کنید. این نسبت از تقسیم چولگی و کشیدگی بر خطای استاندارد آن قابل محاسبه است. اگر عدد حاصل در بازه [۲ و ۲-] قرار گیرد، میتوان توزیع دادهها را نرمال در نظر گرفت.
آزمون چولگی و کشیدگی دادهها در SPSS
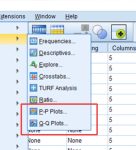
فرمان زیر را در SPSS اجرا کنید:
Analyze/Descriptive Statistics/Descriptive
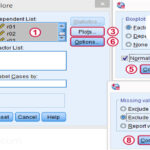
در کادر باز شده متغیرهایی که میخواهید چولگی و کشیدگی آن را آزمون کنید را به کادر سفید انتقال دهید. سپس روی کلید options کلیک کنید و در کادر جدید گزینههای Skewness و kurtosis را فعال کنید. برای مثال به مقادیر جدول زیر دقت کنید:
| Skewness | Kurtosis | |||
| Statistic | Std. Error | Statistic | Std. Error | |
| D1 | ۰.۱۴۶ | ۰.۲۸۷ | ۰.۷۸۴ | ۰.۵۶۶ |
| D2 | -۰.۱۰۹ | ۰.۲۸۷ | -۰.۹۹۴ | ۰.۵۶۶ |
برای متغیر D1 مقدار نسبت چولگی به خطای استاندارد ۰/۵۰۹ و نسبت کورتوسیس ۱/۳۸۵ بدست میآید که در بازه (۲، ۲-) قرار دارد. بنابراین میتوان گفت متغیر D1 نرمال بوده و توزیع آن متقارن است. برای متغیر D2 مقدار نسبت چولگی به خطای استاندارد ۰/۳۸۰ و نسبت کورتوسیس ۱/۷۵۶ بدست میآید که در بازه (۲، ۲-) قرار دارد. بنابراین میتوان گفت توزیع دادههای متغیر D2 نیز نرمال است.
منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: نارون.