پرومته (PROMETHEE) یکی از روشهای تصمیمگیری چندشاخصه برای انتخاب گزینه بهینه است که با تشخیص نوع تابع به سنجش برتری گزینهها میپردازد. این روش توسط دو استاد بلژیکی به نام ژاپن پیر برنز و برتراند مارسکال در دهه ۱۹۸۰ ارائه شد. در نوشتار حاضر روش پرومته برای انتخاب بهترین گزینه آموزش داده شدهاست.
روش پرومته (PROMETHEE)
واژه پرومته (PROMETHEE) سرواژه عبارت Preference Ranking Organization METhod for Enrichment Evaluations میباشد. برگردان پارسی آن «روش سازماندهی به رتبهبندی ترجیحی جهت ارزیابی بهتر» است.
از این روش برای انتخاب بهترین گزینه براساس تعدادی معیار استفاده نمیشود. در ارزیابی تعدادی گزینه براساس تعدادی معیار، باید نوع شاخص، تابع برتری، آستانه بیتفاوتی و آستانه برتری مشخص شود. برای افزایش کارایی «تحلیل هندسی برای کمک متقابل» یا به اختصار تکنیک GAIA استفاده میشود.
این روش دو نوع از اطلاعات را مورد استفاده قرار میدهد:
- اطلاعات برتری: میزان بهتر بودن گزینهها
- اطلاعات مادونی: میزان بدتربودن گزینهها
یعنی گزینهها یکبار براساس میزان بهتر بودن و یک بار براساس میزان بدتر بودن رتبهبندی میشوند. روش پرومته از پیچیدهترین روشهای تصمیمگیری چندمعیاره میباشد که نتایج آن از دقت بسیاری زیادی برخوردار است. این روش با استفاده از نرمافزار ویژوال پرومته دانشجویان رشتههای مدیریت و صنایع میتوانند مسائل تصمیمگیری چندمعیاره که مربوط به درس تحقیق در عملیات میباشد را حل کنند.
گامهای انجام روش پرومته
تشکیل ماتریس تصمیم
نخستین گام در این تکنیک تشکیل ماتریس تصمیم است. ماتریس تصمیمگیری یک ماتریس برای ارزیابی تعدادی گزینه براساس تعدادی معیار است. یعنی ماتریسی که در آن هر گزینه براساس تعدادی معیار امتیازدهی شده است. ماتریس تصمیم با X و هر درایه آن با xij نشان داده میشود.
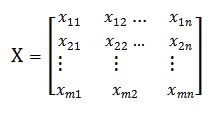
ماتریس تصمیم
تعیین آستانه برتری و بی تفاوتی
قبل از اقدام به تحلیل باید نوع هر معیار (بیشینه یا کمینه)، آستانه برتری، آستانه بیتفاوتی و نوع تابع برتری مشخص شود.
آستانه بیتفاوتی : میزانی از اختلاف که اهمیتی در ارجحیت دو گزینه رقیب نداشته باشد آستانه بیتفاوتی نامیده میشود. بطور قراردادی آستانه بیتفاوتی با حرف q نمایش داده میشود.
آستانه برتری : آستانه برتری میزانی از اختلاف است که به ازای آن یک گزینه نسبت به گزینه رقیب برتری کامل خواهد داشت. بطور قراردادی آستانه برتری با حرف p نمایش داده میشود.
تشخیص نوع تابع
همیشه هم آستانه برتری و آستانه بی تفاوتی وجود ندارد. در برخی موارد ممکن است فقط یکی از این دو وجود داشته باشد بنابراین براساس نوع ارجحیت معیار، از توابع مختلفی استفاده میشود. مهم ترین بخش تکنیک پرومته تشخیص نوع تابع است. انواع توابع روش پرومته PROMETHEE در شکل زیر ارائه شده است.
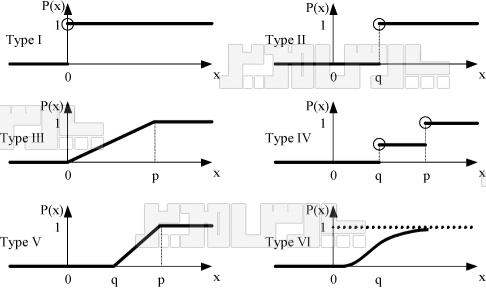
انواع توابع در روش پرومته
موزون کردن ماتریس
پس از آنکه مقادیر آستانه بی تفاوتی، آستانه برتری و نوع تابع مشخص شد باید ماتریس تصمیم موزون شود.
برای این منظور وزن هر معیار در تمامی درایههای زیر همان معیار ضرب میشود. وزن معیارها باید از قبل مشخص شود. برای این منظور معمولاً از تکنیک آنتروپی، فرایند تحلیل سلسلهمراتبی، روش بهترین بدترین (BWM) و روش سوارا SWARA استفاده میشود.

ماتریس تصمیم موزون
تعیین وزن نهایی گزینهها
باید توجه داشت برای شاخصهای Max اگر فاصله منفی باشد برابر صفر خواهد بود. برای شاخصهای Min این رابطه به صورت عکس حاکم است.
ابتدا اختلاف گزینه یک را با سایر گزینهها حساب میکنیم. برای این کار به سادگی عمل تفریق را انجام میدهیم.
در گام دو میزان اختلاف معنادار را با توجه به نوع تابع برتری حساب میکنیم. به علت تنوع در شاخصها امکان خطا در محاسبات دستی زیاد است بنابراین از نرمافزار برای انجام محاسبات استفاده شده است.
در تکنیک PROMETHEE مانند تکنیک پرومته دو نوع از اطلاعات مورد استفاده قرار گیرد: اطلاعات برتری و اطلاعات مادونی. بنابراین پس از محاسبه ماتریسهای ترجیحی و مادونی میتوان ترجیح نهایی گزینهها را محاسبه کرد. براساس جریانهای مثبت و منفی خروجی نرمافزار پرومته میتوان رتبهبندی پایانی را انجام داد.
آموزش کامل روش پرومته
پکیج آموزشی روش پرومته شامل پاورپوینت و فایل آموزشی
- پاورپوینت آموزش روش پرومته شامل ۲۸ اسلاید قابل ویرایش و متن باز
- آموزش حل مسئله با یک مثال کاربردی
سخن پایانی
پرومته یک روش تصمیمگیری چند شاخصه جبرانی است که با مقایسه چندین گزینه براساس چندین معیار به تصمیمگیری کمک میکند. هدف آن است تا براساس توابع مناسب انتخاب بهینه انجام شود آنگونه که تصمیمگیری قابل اتکا باشد. تشخیص نوع تابع مهمترین نکته در ارزیابی گزینهها مهمترین رکن تصمیمگیری است. در این صورت میتوان ارزیابی درستی از گزینهها براساس معیارهای موجود ارائه کرد.
دانلود مقاله آموزش پرومته نوشته برنز و مارسکال
منبع: حبیبی، آرش؛ آفریدی، صنم. کتاب تصمیمگیری چندشاخصه. تهران: ناروندانش.