تعیین حجم نمونه PLS

تعیین حجم نمونه PLS تابع قوانین و اصول روشنی است و نباید اینگونه برداشت شود که روش حداقل مربعات جزیی برای هر حجمی از نمونه قابل استفاده است. حجم نمونه در مدل‌یابی مسیر PLS می‌تواند تا اندازه قابل ملاحظه‌ای کوچک باشد. برای نمونه متغیرها نسبت به مشاهده‌ها بیشتر بوده و ممکن است مقداری از داده‌ها بطور تصادفی بدست نیامده باشد. به دلیل این ویژگی هاست که پژوهشگران، هنگامی که حجم نمونه نسبتاً پایین است از مدل‌سازی مسیر PLS به جای لیزرل استفاده می‌کنند.

تعیین حجم نمونه مناسب بیشتر به اندازه روابط یا سطح توان دلخواه وابسته است. پژوهشگر پیش از تصمیم‌گیری برای انتخاب یک نمونه مناسب باید ویژگی‌های توزیعی داده ها، داده‌های حاصل نشده بالقوه، ویژگی‌های سنجش متغیرهای مورد بررسی و مقدار روابط را مورد توجه قرار دهد، یا اطمینان یابد که واقعاً حجم نمونه کافی برای مطالعه پدیده مورد علاقه در دسترس است.

پرسش و پاسخ پیرامون برآورد حجم نمونه در حداقل مربعات جرئی

پرسش ۱: آیا حداقل مربعات جزئی فقط برای نمونه‌های کوچک قابل استفاده است؟

خیر. این یک برداشت اشتباه است که برخی می‌پندارند حجم نمونه برای حداقل مربعات جزئی حتما باید اندک باشد. دقت کنید «حداقل مربعات جزئی نسبت به حجم نمونه حساسیت کمتری دارد» این به آن معنا نیست که نمونه باید کوچک باشد تا از این روش استفاده کنید.

پرسش ۲: آیا حداقل مربعات جزئی فقط برای هر نمونه‌ای قابل استفاده است؟

خیر. این برداشت اشتباه نیز از همین گزاره ناشی می‌شود: «حداقل مربعات جزئی نسبت به حجم نمونه حساسیت کمتری دارد». درست است که حداقل مربعات جزئی نسبت به حجم نمونه حساسیت چندانی ندارد اما بازهم ملاحظاتی برای تعیین کف نمونه باید در نظر گرفته شود.

با وجود اینکه PLS برای نمونه‌های خیلی کوچک و یا موقعی‌که موارد نسبت به متغیرهای نشانگر کمتر باشد قابل استفاده است، اما تکیه بر نمونه‌های کوچک می‌تواند نتایج ضعیفی فراهم کند. نمونه‌های بزرگتر، برآوردهای PLS را قابل اطمینان تر می‌سازد. بنابراین میانگین میزان خطای مطلق در PLS با افزایش حجم نمونه کاهش می‌یابد. حجم نمونه کوچک برای ضرایب مسیر کوچک کافی نیست، در این صورت حجم نمونه برابر با مدل یابی معادلات ساختاری مورد نیاز است.

تعیین حجم نمونه PLS با روش نمایی گاما

راهکار علمی برای تعیین حجم نمونه حداقل مربعات جزئی، روش نمایی گاما (Gamma exponential method) است. در این روش تعداد نمونه براساس توان آزمون (Power Analysis) و اندازه اثر (Effect Size) تعیین می‌شود. همچنین تعداد سازه‌ها (متغیرهای پنهان) و گویه‌ها (متغیرهای مشاهده‌پذیر) نیز در نظر گرفته می‌شوند [حبیبی و جلال‌نیا، ۱۴۰۱ : ۳۰).

توان آزمون ۸۰% و اندازه اثر نیز ۰/۱۵ در نظر گرفته می‌شود. براساس دیدگاه کوهن (۱۹۸۸) میزان اندازه اثر به ترتیب ۰/۰۲ (ضعیف) ۰/۱۵ (متوسط) و ۰/۳۵ (قوی) تفسیر می‌شود. تعداد سازه‌ها و گویه‌ها نیز به پرسشنامه مورد استفاده بستگی دارد.

در تحلیل توان آماری کوهن برای مدل‌های رگرسیون چندگانه (OLS) آمده است که مدل‌های اندازه‌گیری کیفیتی قابل قبول برحسب بارهای بیرونی دارند. بارهای عاملی باید بالاتر از آستانه مشترک ۰/۷ باشند. برای مطالعه بیشتر آموزش محاسبه حجم نمونه با اندازه اثر و توان آزمون را بنگرید. برای این منظور می‌توانید از نرم‌افزار G*Power استفاده کنید.

تعیین حجم نمونه PLS با روش‌های سرانگشتی

از قواعد سرانگشتی (Rule of thumbs) نیز برای سنجش حجم نمونه استفاده می‌گردد. برای نمونه براساس تعداد روابط میان سازه‌ها حجم نمونه مانند جدول زیر بر آورد می‌گردد. برای نمونه اگر تنها دو رابطه میان سازه‌ها وجود داشته باشد به نمونه‌ای شامل ۵۲ نفر نیاز است.

حجم نمونه حداقل مجذورات جزیی

برخی از پژوهشگران پیشنهاد کرده‌اند از «قاعده ۱۰» استفاده شود. براساس این قاعده، حجم نمونه باید ۱۰ برابر بیشترین رابطه بین سازه‌ها باشد. به دیگر سخن باید ببینید به هر سازه چند پیکان وارد شده است، بیشترین تعداد رابطه را در عدد ۱۰ ضرب کنید تا حجم نمونه برآورد شود. روش‌های سرانگشتی دیگری نیز وجود دارد که هیچکدام راهکار علمی و دقیقی نیستند.

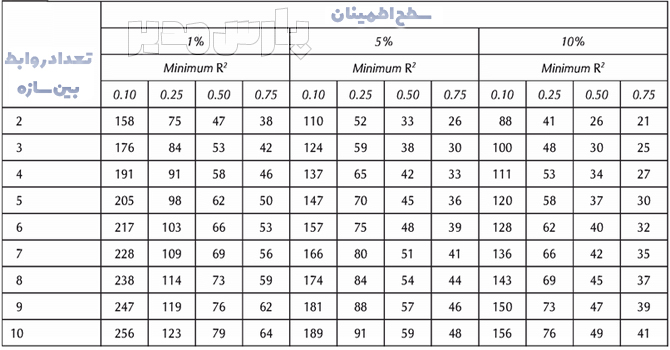
تعیین حجم نمونه PLS با جدول کوهن

کوهن (۱۹۹۲) جدول کاملی برای برآورد حداقل حجم نمونه براساس سطوح خطای گوناگون جهت دستیابی به میزان‌های مختلفی از ضریب تشخیص ارائه کرد. در این جدول حجم نمونه براساس سطح خطای ۱%، ۵% و ۱۰% برای ۲ تا ۱۰ رابطه بین سازه‌ها تعیین می‌گردد. بسته به اینکه پژوهشگر به دنبال چه میزان از ضریب تشخیص باشد می‌توان حجم نمونه را با جدول زیر تعیین کرد. حجم نمونه لازم برای روش حداقل مربعات جزئی در سطح اطمینان ۹۵% با ضریب تشخیص ۲۵% در جدول زیر ارائه شده است.

حداقل حجم نمونه PLS

حداقل حجم نمونه در تکنیک حداقل مجذورات جزیی یا PLS دلخواه نیست. اگرچه با استفاده از تکنیک‌های بوت‌استراپینگ مدل‌های PLS با هر حجمی اجرا می‌شوند اما نتایج و دقت آنها بشدت به حجم نمونه وابسته است. بنابراین در بکارگیری نمونه لازم برای PLS دقت کنید.

تعیین حجم نمونه PLS با روش بارکلای و همکاران

یکی از قواعد شناخته شده برای تعیین حداقل نمونه لازم در روش PLS ، توسط بارکلای و همکاران (۱۹۹۵) ارائه شد. به‌زعم این نویسندگان حداقل حجم نمونه لازم برای استفاده از روش PLS ، برابر است با بزرگترین مقدار حاصل از دوقاعده زیر:

الف) ۱۰ ضرب در تعداد شاخص‌های سازه‌ای که بیشترین شاخص را دارد.

ب) ۱۰ ضرب در بیشترین روابط موجود در بخش ساختاری مدل اصلی پژوهش که به یک متغیر مربوط می‌شوند.

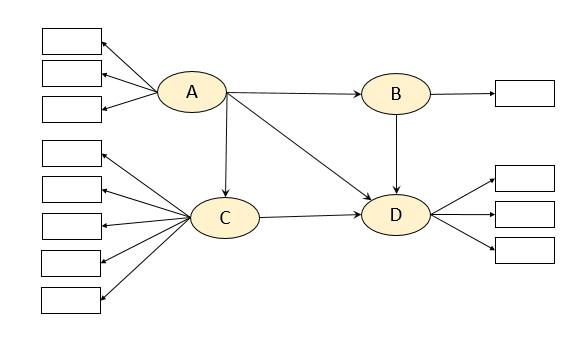
برای روشن تر شدن روش مطرح توسط بارکلای و همکاران، مدل شکل پایین را در نظر بگیرید.

روش بارکلای و همکاران

براساس قاعده اول سازه C شامل ۵ شاخص (متغیر مشاهده‌پذیر) است و بیشترین تعداد شاخص‌ها را دارد. بنابراین براساس قاعده اول ۵ × ۱۰ = ۵۰ نمونه لازم است.

براساس قاعده دوم سازه D و A هر کدام با ۳ رابطه بیشترین رابطه را با دیگر سازه‌ها دارند. بنابراین براساس قاعده دوم ۳ × ۱۰ = ۳۰ نمونه لازم است. پس با توجه به قاعده اول و دوم در این مطالعه بین ۳۰ تا ۵۰ نمونه لازم می‌باشد. البته توجه داشته باشید این روش از منطق آماری قدرتمندی برخوردار نیست و به پژوهشگران پیشنهاد نمی‌شود.

جمع‌بندی

یک اشتباه رایج در حداقل مربعات جزئی آن است که پژوهشگران گمان می‌کنند با هر میزان اندکی از نمونه می‌توانند از این روش بهره گیرند. این درست است که روش حداقل مربعات جزئی به حجم نمونه حساسیت چندانی ندارد. اما توجه کنید نباید از این گزاره برداشت نادرستی صورت گیرد. محاسبه حجم نمونه مناسب برای حداقل مربعات جزئی تابع قواعد و قوانین روشنی است که باید لحاظ شود. راهکارهایی برای این منظور در این نوشتار ارائه گردید. با این وجود پیشنهاد می‌شود از راهکار توان آزمون و اندازه اثر استفاده کنید.

فهرست منابع

حبیبی، آرش؛ جلال‌نیا، راحله. (۱۴۰۱). کتاب حداقل مربعات جزئی. تهران: نارون.

Barclay, D., Higgins, C., & Thompson, R. (1995). The partial least squares (PLS) approach to causal modeling: Personal computer adoption and use as an illustration, Technology Studies 2 (2): 285–۳۰۹. View at.

Cohen, J. (1992). A power primer. Psychological bulletin, 112(1), 155.

Hair Jr, J. F., Hult, G. T. M., Ringle, C., & Sarstedt, M. (2013). A primer on partial least squares structural equation modeling (PLS-SEM). Sage Publications.