کوداس (CODAS) یکی از روشهای تصمیمگیری چندشاخصه برای انتخاب بهترین گزینه براساس فاصله اقلیدسی و فاصله تاکسی از نقطه ایدهآل منفی است. این روش نیز مانند بسیاری از روشهای تصمیمگیری چندمعیاره با هدف انتخاب بهترین گزینه طراحی شد. یک مثال عددی در این مقاله استفاده شده است تا درک بهتری از روش کوداس در حل مسائل واقعی بدست آید.
روش کوداس (CODAS)
روش کوداس (ارزیابی ترکیبی مبتنی بر فاصله) یا COmbinative Distance-based Assessment بوسیله زاوادساکاس و همکارانش به سال ۲۰۱۶ پیشنهاد شد. هدف این روش انتخاب بهترین گزینه براساس تعدادی معیار است.
در روش CODAS بهترین گزینه آن است که بیشترین فاصله را از عوامل منفی داشته باشد. از این منظر شاید بتوان این روش را با تکنیک تاپسیس مقایسه کرد که فاصله از معیارهای منفی را نیز در نظر میگیرد.
ابتدا از فاصله اقلیدسی استفاده میشود و سپس فاصله تاکسی Taxicab استفاده میشود. این فاصلهها براساس اختلاف با نقطه ایدهآل منفی محاسبه میشوند. هر گزینهای که بیشترین فاصله را با ایدهآل منفی داشته باشد بهترین گزینه در تکنیک کوداس میباشد.
گامهای روش کوداس (CODAS)
هدف: انتخاب بهترین گزینه براساس تعدادی شاخص
الزامات: باید اوزان شاخصها مشخص شده باشد.
الگوریتم اجرایی تکنیک کوداس CODAS به صورت زیر است:
تشکیل ماتریس تصمیم
نخستین گام در این تکنیک تشکیل ماتریس تصمیم است. ماتریس تصمیمگیری یک ماتریس برای ارزیابی تعدادی گزینه براساس تعدادی معیار است. یعنی ماتریسی که در آن هر گزینه براساس تعدادی معیار امتیازدهی شده است. ماتریس تصمیم با X و هر درایه آن با xij نشان داده میشود.
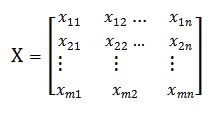
ماتریس تصمیم
تشکیل ماتریس تصمیم نرمال
نرمال سازی یا بی مقیاس سازی دومین گام در حل تمامی تکنیکهای تصمیمگیری چندمعیاره مبتنی بر ماتریس تصمیم است. در روشهای MCDM بهتر است از واژه بیمقیاس سازی استفاده شود. در تکنیک CODAS نرمال سازی به روش رومینا صورت میگیرد.. اگر ماتریس تصمیم با X و هر درایه آن با نشان داده شود ماتریس تصمیم نرمال با و هر درایه ماتریس بیمقیاس شده با نشان میدهند.

نرمال سازی به روش رومینا
ماتریس تصمیم نرمال شده به صورت زیر نمایش داده میشود:

ماتریس تصمیم نرمال شده
تشکیل ماتریس تصمیم نرمال موزون
در گام سوم از تکنیک کوداس CODAS باید ماتریس تصمیم نرمال ایجاد شده، موزون شود. برای این منظور وزن هر معیار در تمامی درایههای زیر همان معیار ضرب میشود. وزن معیارها باید از قبل مشخص شود. برای این منظور معمولاً از تکنیک آنتروپی شانون، فرایند تحلیل سلسلهمراتبی (AHP)، روش بهترین بدترین (BWM) و روش سوارا SWARA استفاده میشود.

ماتریس تصمیم نرمال موزون
محاسبه نقطهایده آل منفی
پس از تشکیل ماتریس نرمال موزون زمان محاسبه نقطهایده آل منفی Negative-ideal solution است. ایدهآل منفی هرمعیار با نمایش داده شده و به صورت زیر محاسبه میشود:
NSj=Min Vij
کوچکترین مقدار هر معیار در ماتریس نرمال موزون را به عنوان نقطهایده آل منفی انتخاب میکنیم.
محاسبه میزان مطلوبیت هر گزینه
برای تعیین میزان مطلوبیت هر گزینه ابتدا میزان دوری هر گزینه از ایدهآل منفی با استفاده از دو نوع فاصله محاسبه میشود:
- فاصله اقلیدسی
- فاصله منهتن یا فاصله تاکسی

برای انتخاب گزینه بهینه از رابطه زیر استفاده میشود:
Hik = (Ei – Ek) + (𝜓 (Ei – Ek) × (Ti – Tk))
مقدار پارامتر 𝜓 (بخوانید پسی Psi) براساس میزان آستانه 𝜏 (بخوانید تاو Tau) تعیین میشود. هرچه مقدار H هر گزینه بیشتر باشد آن گزینه از اولویت بیشتری برخوردار است.
آموزش روش کوداس (CODAS) در فایل اکسل
یک نمونه مثال حل شده از تکنیک کوداس (CODAS) ر فایل اکسل
آموزش کامل مثال حل شده بصورت فارسی در یک فایل ضمیمه
توجه: این یک کتاب حجیم نیست یک فایل ساده است که بصورت کوتاه و اصولی روش کوداس CODAS را تشریح کرده است.
سخن پایانی
تکنیک کوداس (CODAS) یکی از روشهای نوین تصمیمگیری چندمعیاره است که بر پایه سنجش فاصلهٔ گزینهها از راهحل ایدهآل و ضدایدهآل طراحی شد. این روش با ترکیب دو نوع فاصله اقلیدسی و تاکسیمتری، توانایی بالایی در رتبهبندی گزینهها و تشخیص گزینه برتر دارد. کوداس نسبت به تغییرات وزن معیارها حساسیت کمی دارد و در مقایسه با روشهایی مانند تاپسیس یا ویکور، پایداری بیشتری در نتایج نشان میدهد. همچنین قابلیت توسعهٔ آن به محیطهای فازی و شهودی باعث شد در پژوهشهای مدیریتی، مهندسی و تصمیمگیری پیچیده بهعنوان ابزاری دقیق و کارآمد برای تحلیل گزینهها در شرایط عدم قطعیت مورد توجه قرار گیرد.