تحلیل عاملی تاییدی

تحلیل عاملی تاییدی (Confirmatory Factor Analysis) روشی است که نشان می‌دهد چه میزان گویه‌های سنجش یک سازه به درستی انتخاب شده‌اند. در واقع در این روش مشخص می‌شود آیا سوالاتی که در یک پرسشنامه برای سنجش هر عامل انتخاب شده است مناسب می‌باشد یا خیر. بنابراین تحلیل عاملی تائیدی یک ابزار سنجش روایی پرسشنامه است و به روایی سازه یا مدل اندازه گیری نیز موسوم است.

انواع تحلیل عامـلی

بطور کلی تحلیل عاملی (Factor Analysis) جهت پی بردن به متغیرهای زیر بنایی یک پدیده یا اطمینان از گویه‌های سنجش عوامل استفاده می‌شود. داده‌های اولیه برای فاکتور آنالیز، ماتریس همبستگی بین متغیرها است. در این روش، متغیرهای وابسته وجود ندارد و هدف بررسی روابط متغیرهای پنهان نیست. بلکه هدف بررسی و تعیین رابطه متغیر پنهان و آشکار است.

به طور کلی فاکتور آنالیز دو دسته کلی تقسیم می‌شود:

• تحلیل عاملی تاییدی
• تحلیل عاملی اکتشافی

تحلیل عاملی اکتشافی (EFA) : اگر تعدادی گویه وجود داشته باشد و بخواهید این گویه‌ها را در چند عامل بزرگتر دسته بندی کنید از تحلیل عاملی اکتشافی استفاده می‌شود. برای مثال بعد از یک تحقیق کیفی گویه‌هایی که ار مصاحبه‌ها استخراج شده است را با فاکتور آنالیز اکتشافی خوشه‌بندی می‌کنند.

تحلیل عاملی تاییدی (CFA) : در فاکتور آنالیز تائیدی هدف اطمینان از بک ساختار عاملی منظم است. وقتی شما برای عوامل اصلی تحقیق خود گویه هایی را شناسایی کرده اید برای اطمینان از ساختار عاملی موجود از تحلیل عاملی تائیدی استفاده می‌شود.

انواع تحلیل عاملی تائیدی

روش تحلیل عاملی تاییدی خود دو دسته اصلی دارد:

• تحلیل عاملی تاییدی مرتبه اول
• تحلیل عاملی تاییدی مرتبه دوم

هریک از این روش‌ها در ادامه تشریح می‌گردد.

تحلیل عاملی تاییدی مرتبه اول

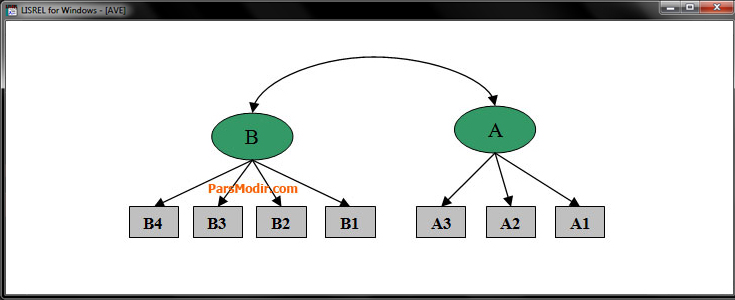
در تحلیل عاملی تاییدی مرتبه اول یا First order confirmatory factor analysis رابطه عامل یا عامل‌ها (متغیرهای پنهان) با گویه‌ها (متغیرهای مشاهده‌پذیر) مورد سنجش قرار می‌گیرد. در این روش هیچ‌گونه رابطه‌ای بین متغیرهای پنهان مورد بررسی قرار نمی‌گیرد. این نوع مدل اندازه‌گیری صرفاً برای اطمینان از آن است که متغیرهای پنهان درست اندازه‌گیری شده‌اند. در فاکتور آنالیز تائیدی مرتبه اول می‌توان رابطه یک عامل با چند گویه یا چندعامل با چند گویه را مورد بررسی قرار داد.

تحلیل عاملی تاییدی مرتبه اول

تحلیل عاملی تاییدی مرتبه دوم

در تحلیل عاملی تاییدی مرتبه دوم یا Second order confirmatory factor analysis زمانی که یک سازه بزرگ خود از چند متغیر پنهان تشکیل شده باشد، استفاده می‌شود. در این روش علاوه بر بررسی رابطه متغیرهای مشاهده‌پذیر با متغیرهای پنهان، رابطه متغیرهای پنهان با سازه اصلی خود نیز بررسی می‌شود.

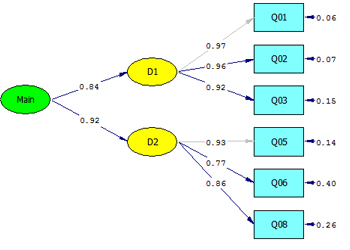
تحلیل عاملی تاییدی مرتبه دوم

تحلیل عاملی تاییدی مرتبه سوم

در این روش یک سازه اصلی به چند سازه فرعی تقسیم می‌شود. سازه‌های فرعی خود به چند سازه فرعی دیگر تقسیم می‌شوند. برای سازه‌های سطح آخر تعدادی سوال یا گویه مطرح می‌شود.

  نرم‌افزار لیزرل و اموس قادر به انجام تحلیل عاملی تاییدی مرتبه سوم نیستند و این روش فقط در تئوری مطرح شده است. در مورد صحت تئوریک فاکتور آنالیز تائیدی مرتبه سوم نیز شبهات زیادی مطرح است. مطمئن باشید اگر خروجی در مقالات دیدید جادوی فتوشاپ است!

تفسیر نتایج

برای تفسیر نتایج تحلیل عاملی تاییدی باید با دو مقوله آشنا باشید:

• بار عاملی (Factor Loading)
• آماره تی (T-Value)

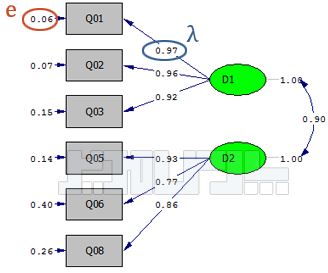
قدرت رابطه بین عامل (متغیر پنهان) و متغیر قابل مشاهده بوسیله بار عاملی نشان داده می‌شود. به شکل تحلیل عامـلی تاییدی مرتبه اول توجه کنید. بار عاملی در این شکل با λ نشان داده شده است. بار عاملی مقداری بین صفر و یک است. اگر بار عاملی کمتر از ۰.۳ باشد رابطه ضعیف درنظر گرفته شده و از آن صرف‌نظر می‌شود. بارعاملی بین ۰.۳ تا ۰.۶ قابل قبول است و اگر بزرگتر از ۰.۶ باشد خیلی مطلوب است.

بسیار مهم: در برخی منابع حداقل مقدار قابل قبول ۰/۴ و در برخی منابع ۰/۵ ذکر شده است. تمامی این مقادیر تجربی بوده و جنبه پیشنهادی دارند. دقت کنید مقدار بارعاملی ملاک معنادار بودن آن نیست و باید آماره t بررسی شود. تمامی مقادیری که آماره t برای آنها بالای ۱/۹۶ باشند از نظر آماری معنادار هستند. بهترین راه آن است روایی همگرا را برای هر عامل حساب کنید اگر از ۰/۵ کوچکتر بود اقدام به حذف گویه‌هایی که بارعاملی کمتری دارند کنید تا مقدار AVE از ۰/۵ بیشتر شود.
آرش حبیبی

در نرم‌افزار لیزرل بار عاملی از طریق گزینه Standardized solution از لیست Estimates محاسبه می‌شود. در فاکتور آنالیز متغیرهائی که یک متغیر پنهان (عامل) را می‌سنجند، باید با آن عامل، بار عاملی بالا داشته باشند (روایی همگرا) و با سایر عامل‌ها، بار عاملی پائین داشته باشند (روایی واگرا).

جهت بررسی معنادار بودن رابطه بین متغیرها از آماره آزمون t یا همان t-value استفاده می‌شود. چون معناداری در سطح خطای ۰.۰۵ بررسی می‌شود بنابراین اگر میزان بارهای عاملی مشاهده شده با آزمون t-value از ۱/۹۶ کوچکتر محاسبه شود، رابطه معنادار نیست و در نرم‌افزار لیزرل با رنگ قرمز نمایش داده خواهد شد.

تفسیر نتایج در نرم‌افزار اموس

نتایج حاصل از فاکتور آنالیز نرم‌افزار اموس (AMOS) به صورت یک جدول رگرسیون شامل موارد زیر است:

• بارعاملی (Estimate)
• خطای استاندارد (Standard Error SE)
• آماره تی (Critical ratios CR)
• مقدار معناداری (P)

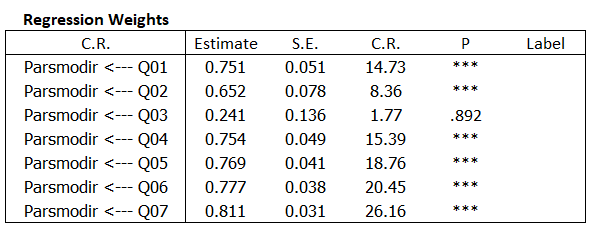
تفسیر نتایج در نرم‌افزار اموس

بارهای عاملی استاندارد در زیر ستون Estimate نمایش داده می‌شود. این مقادیر بهتر است از ۰.۵ بیشتر باشد البته ملاک تصمیم‌گیری مقدار آماره تی و روایی همگرای گویه‌ها است.

آماره تی با عنوان نسبت بحرانی یا CR شناخته می‌شود. این مقدار بهتر است بزرگتر از ۱.۹۶ یا براساس برخی منابع دیگر بزرگتر ۱.۹۸ باشد.

خطای استاندارد یا SE نیز آماره‌ای برای محاسبه آماره تی است. از تقسیم بارعاملی استاندارد بر خطای استاندارد مقدار نسبت بحرانی بدست می‌آید.

در نهایت P-value همان مقدار معناداری است که برای بارهای عاملی معنادار به صورت *** نمایش داده می‌شود.

خلاصه و جمع‌بندی

تحلیل عاملی تائیدی روشی برای شناخت عامل‌ها و گویه‌های تشکیل دهنده یک سازه اصلی است. اگر پژوهشگر بتواند عوامل و گویه‌هایی برای سنجش آنها شناسایی کند با استفاده از این روش می‌تواند ادعای خود را راستی آزمایی کند. به دیگر سخن فاکتور آنالیز یک روش سنجش روایی ابزار اندازه‌گیری است که گاه با عنوان روایی سازه از آن یاد می‌شود. این روش می‌تواند در سطح سازه‌ها و گویه‌ها یا مرتبه‌های بالاتر انجام شود. برای انجام تحلیل عاملی تائیدی می‌توان از نرم‌افزار لیزرل و اموس استفاده کرد.

منبع: حبیبی، آرش؛ کلاهی، بهاره. (۱۴۰۱). کتاب مدل یابی معادلات ساختاری. تهران: جهاد دانشگاهی، چاپ دوم.