پایایی ترکیبی

پایایی ترکیبی (Composite reliability) یک معیار ارزیابی برازش درونی مدل است و براساس میزان سازگاری سوالات مربوط به سنجش هر عامل قابل محاسبه است. این نوع پایایی شباهت زیادی به روایی همگرا دارد و از همان پارامترهای روایی همگرا برای محاسبه پایایی مرکب استفاده می‌شود.

مقایسه آلفای کرونباخ و پایایی ترکیبی

پایایی پرسشنامه به زبان ساده یعنی اینکه ابزار اندازه‌گیری در مکان دیگر یا زمان دیگر نتایج مشابهی بدست دهد. معیار سنتی محاسبه پایایی آلفای کرونباخ است. آلفای کرونباخ براساس میزان پراکنش داده‌ها تعیین می‌شود و انحراف معیار عامل اصلی سنجش پایایی است. از سوی دیگر پایایی ترکیبی براساس هماهنگی درونی سوالات هر عامل محاسبه می‌شود بنابراین معیار دقیق تری است.

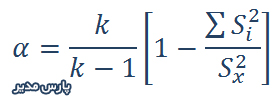
فرمول محاسبه آلفای کرونباخ

محاسبه پایایی ترکیبی

برای محاسبه پایایی مرکب در نرم‌افزار لیزرل و اموس باید از فرمول پایایی ترکیبی مندرج در شکل فوق استفاده کنید. اصول محاسبه پایایی مرکب در نرم‌افزار PLS و تکنیک حداقل مجذورات جزیی نیز ثابت است ولی این نرم‌افزار برخلاف لیزرل مقدار CR را بدست می‌دهد و نیازی نیست با دست آن را محاسبه کنید. برای محاسبه پایایی ترکیبی در نرم‌افزار PLS  کافی است به خروجی این نرم‌افزار رجوع کنید.

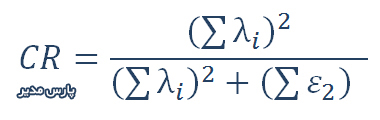
فرمول محاسبه پایایی ترکیبی

پایایی مرکب یا CR مخفف Composite Reliability می‌باشد. روایی همگرا زمانی وجود دارد که CR از ۰/۷ بزرگتر باشد. همچنین CR باید از AVE بزرگتر باشد. در اینصورت هر شرط روایی همگرا وجود خواهد داشت. بطور خلاصه داریم:

CR > 0.7
CR > AVE
AVE > 0.5

با استفاده از بارهای عاملی به سادگی می‌توان پایایی مرکب را در نرم‌افزار لیزرل محاسبه کرد. روی لینک محاسبه آنلاین پایایی ترکیبی کلیک کنید.

ضریب پایایی همگون Rho

میزان پایایی با استفاده از فرمولی که توسط یورسکاگ ارائه شده نیز قابل محاسبه است. ضریب Rho نیز برای سنجش پایایی درونی سازه‌ها است. همچنان که چین (۱۹۹۸) معتقد است ضریب Rho نسبت به آلفای کرونباخ از اطمینان بیشتری برخوردار است. به ضریب Rho گاهی ضریب دایلون-گولداشتین Dillon-Goldstein نیز گفته می‌شود. مقدار این ضریب باید بیش از ۰/۷ باشد. در نسخه شماره سه از نرم‌افزار Smart PLS این مقدار گزارش می‌شود.

منبع: حبیبی، آرش؛ کلاهی، بهاره. (۱۴۰۱). مدل‌یابی معادلات ساختاری و تحلیل عاملی. تهران: جهاد دانشگاهی، چاپ دوم.