بوت‌استراپینگ در حداقل مربعات جزئی

بوت‌استراپینگ (Bootstrapping) در حداقل مربعات جزئی یک شیوه خودگردان سازی یا استفاده مجدد از نمونه برای برآورد آماره تی و سنجش معناداری روابط است. به دیگر سخن، بوت‌استراپینگ آماره آزمون برای سنجش معناداری روابط میان متغیرها را محاسبه می‌کند.

حداقل مربعات جزئی فرض توزیع نرمال داده‌ها را ندارد به این معنی که آزمون معناداری پارامترها در تحلیل رگرسیون را نمی‌توان برای آزمون اینکه آیا ضرائبی نظیر وزن‌ها بیرونی، بارهای بیرونی و ضرائب مسیر، معنادار هستند، بکار برد. در عوض حداقل مربعات جزئی برای آزمون معناداری پارامترها بر رویه ناپارامتریک بوت استراپ تکیه کرده است.

در  روش بوت استرپ تعداد زیادی زیر نمونه (نمونه‌های بوت استراپ) به روش جایگذاری بیرون کشیده می‌شود. جایگذاری به این معنا که هر زمان یک مشاهده به صورت تصادفی از جامعه نمونه‌گیری بیرون کشیده شد، قبل از بیرون شدن مشاهده بعدی، به جامعه نمونه‌گیری بر می‌گردد. یعنی جامعه‌ای که مشاهدات از آن استخراج می‌شود، همواره حاوی عناصر مشابه است. بنابراین یک مشاهده می‌تواند بیش از یک مرتبه انتخاب شود یا در تمام زیرنمونه‌ها اصلا انتخاب نشود. تعداد نمونه‌های بوت‌استرپ باید بالا باشد اما باید حداقل برابر با تعداد مشاهدات معتبر در مجموع داده‌ها باشد. در نتیجه ۵۰۰۰ نمونه بوت‌استراپ پیشنهاد می‌شود.

بوت‌استراپینگ در نرم‌افزار PLS

اگر از توضیحات دکتر آذر در زمینه بوت‌استراپینگ خیلی سر در نیاوردید من با یک مثال این روش را برای شما توضیح می‌دهم. بوت‌استراپ Bootstrap همانطور که از نامش پیدا است به معنای تسمه پوتین و معادل آن در فارسی خودگردان‌سازی است. همانطور که شما تسمه پوتین را می‌کشید تا پوتین در پای شما جا بیفتد، رویه‌های مبتنی بر بوت‌استراپینگ نیز کمک می‌کنند تا یک مقوله دشوار برای محاسبات نرم‌افزاری، ساده شود.

تسمه پوتین (بوت‌استراپ)

کاربرد اصلی بوت‌استراپ در حداقل مربعات جزئی سنجش معناداری روابط میان متغیرها است. بعد از اینکه مدل را ترسیم کردید برای اجرای بوت‌استراپینگ از منوی Calculate گزینه bootstrapping را انتخاب کنید. همچنین در نوار ابزار نیز می‌توانید به صورت زیر از bootstrapping استفاده کنید:

مسیر bootstrapping

با اجرای این دستور آماره آزمون معادل آماره t-value در نرم‌افزار لیزرل و اموس محاسبه شده و برای تمامی روابط نمایش داده می‌شود. یک نمونه از خروجی دستور بوت‌استراپینگ در نرم‌افزار حداقل مربعات جزئی به صورا زیر است:

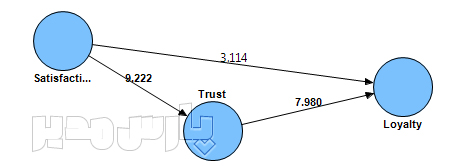
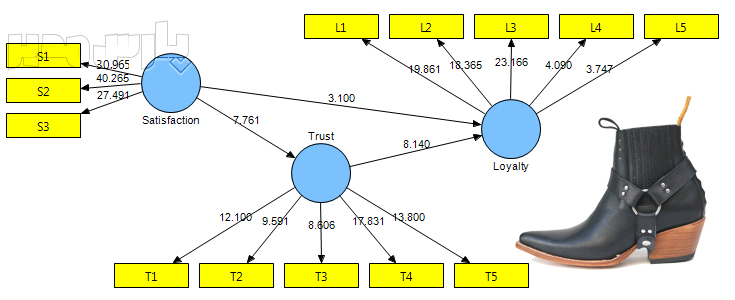
خروجی بوت‌استراپینگ در نرم‌افزار حداقل مربعات جزئی

اعداد روی پیکان اتصال متغیرها به یکدیگر معادل همان آماره t می‌باشد. در سطح اطمینان ۹۵% چنانچه مقدار آماره آزمون از ۱/۹۶ بزرگتر باشد آن رابطه معنادار است. برای مثال آماره آزمون معناداری رابطه رضایت و وفاداری ۳/۱۱۴ بدست آمده است که از مقدار بحرانی ۱/۹۶ بزرگتر است بنابراین رابطه رضایت و وفاداری معنادار است (آرش حبیبی، پارس‌مدیر).

روند تحلیل بوت‌استراپینگ

در بوت‌استراپ لازم است توجه داشته باشید اندازه هر نمونه بوت‌استراپ باید صریحاً مشخص شود. دستورالعمل پذیرفته شده این است که هر نمونه از بوت‌استراپ باید تعداد مشابهی مشاهده نسبت نمونه اصلی داشته باشد. معمولا در ماژول بوت استراپ نرم‌افزار Smart PLS موارد بوت‌استراپ نامیده می‌شود. برای مثال اگر نمونه اصلی دارای ۱۳۰ مشاهده معتبر باشد، هرکدام از ۵۰۰۰ نمونه بوت‌استراپ باید شامل ۱۳۰ مورد باشد. در غیر اینصورت، نتایج آزمون معناداری به صورت سیستماتیک دارای اریبی هستند.

توجه داشته باشید که وقتی از جایگذاری مورد به مورد برای برخورد با مقادیر گم شده استفاده می‌شود، بسیار مهم است که از تعداد نهایی مشاهدات که برای برآورد مدل استفاده می‌شود، مطلع باشید. نمونه‌های بوت‌استراپ برای برآورد مدل مسیری حداقل مربعات جزئی استفاده می‌شود. یعنی، وقتی از ۵۰۰۰ نمونه بوت استراپ استفاده می‌شود، ۵۰۰۰ مدل مسیری حداقل مربعات جزئی برآورد می‌شود.

فاصله اطمینان بوت‌استراپ

تنها به جای گزارش معناداری پارامتر، گزارش فاصله اطمینان بوت‌استراپ که اطلاعات بیشتری در مورد ثبات برآورد یک ضریب فراهم می‌کند، ارزشمند است. فاصله اطمینان، دامنه‌ای است که در آن پارامتر واقعی جامعه با فرض سطح معینی از اطمینان (برای مثال ۹۵%) در آن قرار می‌گیرد.

در زمینه حداقل مربعات جزئی نیز درباره فاصله اطمینان بوت‌استراپ صحبت می‌شود زیرا ساخت فاصله، براساس خطاهای معیار بدست آمده از رویه بوت‌استراپینگ است. بسط این رویکرد، آزمون معناداری شامل فاصله اطمینان بوت‌استراپینگ اصلاح شده هنسلر و همکاران می‌باشد. از آنجاییکه فواصل اطمیان بوت‌استراپ و فواصل بوت‌استراپ اصلاح شده اریبی معمولاً زیاد متفاوت نیستند، مقاله هنسلر و همکاران پیشنهاد می‌شود.