آزمون نرمال بودن دادهها روشی برای تشخیص آن است که مشخص شود توزیع دادههای گردآوری شده از توزیع طیبیعی یا نرمال برخوردار است. قبل از هر گونه آزمونی که با فرض نرمال بودن دادهها صورت میگیرد باید آزمون نرمال بودن صورت گیرد. برای این منظور روشهای متعددی وجود دارد.
در آمار استنباطی شرط اصلی برای انواع آزمونهای آمار پارامتریک و ناپارامتریک به توزیع دادهها بستگی دارد. اگر توزیع دادهها نرمال باشد در اینصورت از روشهای پارامتریک استفاده میشود و اگر نرمال نباشد نباید از روشهای پارامتریک استفاده شود. آزمونهای ناپارامتریک ربطی به توزیع دادهها ندارد. برخی از آزمونهای بررسی نرمال بودن دادهها عبارتند از:
کاربرد چولگی و کشیدگی در آزمون نرمال بودن دادهها
بهترین روش برای دادههای طیف لیکرت و پرسشنامه بررسی چولگی و کشیدگی دادهها است. چولگی معیاری از تقارن یا عدم تقارن تابع توزیع میباشد. برای یک توزیع کاملاً متقارن چولگی صفر و برای یک توزیع نامتقارن با کشیدگی به سمت مقادیر بالاتر چولگی مثبت و برای توزیع نامتقارن با کشیدگی به سمت مقادیر کوچکتر مقدار چولگی منفی است. کشیدگی یا Kurtosis نشان دهنده ارتفاع یک توزیع است. به عبارت دیگر کشیدگی معیاری از بلندی منحنی در نقطه ماکزیمم است و مقدار کشیدگی برای توزیع نرمال برابر ۳ میباشد. کشیدگی مثبت یعنی قله توزیع مورد نظر از توزیع نرمال بالاتر و کشیدگی منفی نشانه پایین تر بودن قله از توزیع نرمال است. برای مثال در توزیع t که پراکندگی دادهها بیشتر از توزیع نرمال است، ارتفاع منحنی کوتاه تر از منحنی نرمال است.
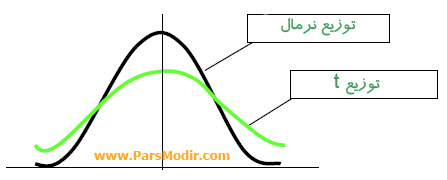
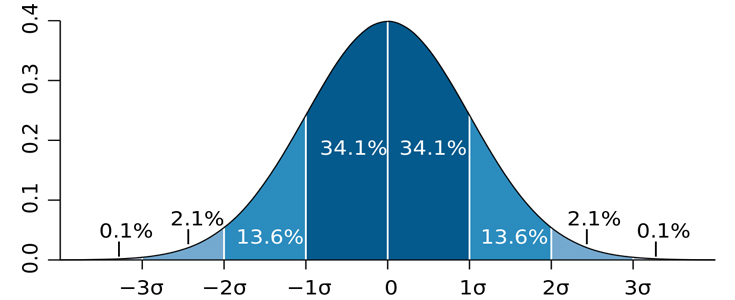
بررسی کشیدگی توزیع نرمال
در حالت کلی چنانچه نسبت چولگی و کشیدگی به خطای استاندارد در بازه (۲، ۲-) باشد دادهها از توزیع نرمال برخوردار هستند.
فرمان زیر را در SPSS اجرا کنید:
Analyze/Descriptive Statistics/Descriptive
در کادر باز شده متغیرهایی که میخواهید چولگی و کشیدگی آن را آزمون کنید را به کادر سفید انتقال دهید. سپس روی کلید options کلیک کنید و در کادر جدید گزینههای Skewness و Kurtosis را فعال کنید. برای مثال به مقادیر جدول زیر دقت کنید:
| Skewness | Kurtosis | |||
| Statistic | Std. Error | Statistic | Std. Error | |
| D1 | ۰.۱۴۶ | ۰.۲۸۷ | ۰.۷۸۴ | ۰.۵۶۶ |
| D2 | -۰.۱۰۹ | ۰.۲۸۷ | -۰.۹۹۴ | ۰.۵۶۶ |
برای متغیر D1 مقدار نسبت چولگی به خطای استاندارد ۰/۵۰۹ و نسبت کورتوسیس ۱/۳۸۵ بدست میآید که در بازه (۲، ۲-) قرار دارد. بنابراین میتوان گفت متغیر D1 نرمال بوده و توزیع آن متقارن است. برای متغیر D2 مقدار نسبت چولگی به خطای استاندارد ۰/۳۸۰ و نسبت کورتوسیس ۱/۷۵۶ بدست میآید که در بازه (۲، ۲-) قرار دارد. بنابراین میتوان گفت توزیع دادههای متغیر D2 نیز نرمال است.
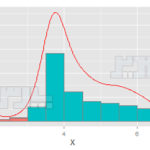
رسم نمودار هیستوگرام برای آزمون نرمال بودن دادهها
ترسیم نمودار هیستوگرام از روشهای آزمون نرمال بودن دادهها است. با استفاده از نرمافزار SPSS به سادگی میتوان نمودار هیستوگرام با نمایش منحنی نرمال را ترسیم کرد. فرمان زیر را در SPSS اجرا کنید:
Analyze/ Descriptive Statistics/ Frequencies
در کادر باز شده متغیرهایی که میخواهید منحنی نرمال را برای آن ترسیم کنید به کادر سفید انتقال دهید. سپس روی کلید Charts کلیک کنید و در کادر جدید گزینههای Histograms و with normal curve را فعال کنید. منحنی نرمال و نمودار هسیتوگرام به نمایش در خواهد آمد.
آزمون کولموگروف-اسمیرنوف
علاوه بر بررسی عادی یا نرمال بودن کشیدگی و یا چولگی توزیع دادهها، از آزمون شاپیرو-ویلک یا آزمون کولموگروف-اسمیرنوف استفاده میشود برای آزمون نرمال بودن دادهها استفاده میشود.
هنگام بررسی نرمال بودن دادهها ما فرض صفر مبتنی بر اینکه توزیع دادهها نرمال است را در سطح خطای ۵% تست میکنیم. بنابراین اگر آماره آزمون بزرگتر مساوی ۰.۰۵ بدست آید، در این صورت دلیلی برای رد فرض صفر مبتنی بر اینکه داده نرمال است، وجود نخواهد داشت. به عبارت دیگر توزیع دادهها نرمال خواهد بود. برای آزمون نرمالیته فرضهای آماری به صورت زیر تنظیم میشود:
H0 : توزیع دادههای مربوط به هر یک از متغیرها نرمال است
H1 : توزیع دادههای مربوط به هر یک از متغیرها نرمال نیست
جهت انجام این دو آزمون فرمان زیر را اجرا کنید:
Analyze/Descriptive Statistics/Explore
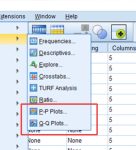
در کادر باز شده متغیرهای موردنظر را وارد لیست Dependent list کنید و سایر جاها را خالی بگذارید. سپس روی دکمه plots کلیک کرده و در کادر جدید گزینه Normality plots with tests را تیک دار کنید.
با این عمل خروجی شامل جدولی تحت عنوان Tests of Normality است که به شما دو مقدار سطح معناداری را برای هر کدام از متغیرها به طور مجزا میدهد. این مقادیر در تشخیص نرمال بودن دادهها تعیین کننده است. چنانچه سطح معناداری در آزمون Shapiro-Wilk یا آزمون کولموگروف-اسمیرنوف که در این جدول با sig. نمایش داده میشود بیشتر از ۰.۰۵ باشد میتوان دادهها را با اطمینان بالایی نرمال فرض کرد. در غیر این صورت نمیتوان گفت که دادهها توزیعشان نرمال است.
برای درک بیشتر آزمون نرمال بودن دادهها پیشنهاد میشود آزمون تصادفی بودن داده ها را مطالعه کنید.
ملاک آزمون نرمال بودن دادهها چیست؟
وقتی پژوهشگران از طیف لیکرت برای گردآوری دادهها استفاده میکنند با یک مشکل بزرگ مواجه هستند. برای استفاده از آزمونهای پارامتریک مانند همبستگی پیرسون، رگرسیون، مدل ساختاری و آزمون تی، توزیع دادهها باید نرمال باشد. بهطور مرسوم برای بررسی نرمال بودن از آزمون کولموگروف-اسمیرنوف استفاده میشود. اما نتیجه همیشه ناامید کننده است. نتایج این آزمون نشان میدهد دادهها نرمال نیست. در پاسخ باید گفت استفاده از این آزمون برای دادههای آماری کوچک (کمتر از ۳۰ داده) مناسب است. دوم اینکه استفاده از این آزمون برای دادههای طیف لیکرت مورد تردید است. توصیه شده است از آزمون KS برای پرسشنامههای طیف لیکرت استفاده نشود.
Keller, G. (2015). Statistics for Management and Economics, Abbreviated. Cengage Learning.
Levin, R. I. (2011). Statistics for management. Pearson Education India.
پرسش دوم این است که نتایج آزمون چولگی و کشیدگی دادهها با نتایج آزمون KS همخوانی ندارد. یکی نشان میدهد دادهها نرمال است و یکی خلاف این ادعا را نشان میدهد. تکلیف چیست؟ پاسخ بسیار ساده است. هرگز از آزمون کولموگروف-اسمیرنوف برای بررسی نرمال بودن دادهها استفاده نکنید. براساس کتاب آمار کاربردی مدیریت نوشته کلر (۲۰۱۵) و لوین (۲۰۱۱) بهتر است چولگی و کشیدگی دادهها بررسی شود. همچنین آزمون شاپیرو-ولیک نیز برای دادههای طیف لیکرت مناسب نیست.
منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: نارون.