ماتریس تکین (Singular matrix)

ماتریس تکین (Singular matrix) به ماتریسی گفته می‌شود که دترمینان آن صفر است و از همین‌رو قابل معکوس کردن نیست. به‌همین ترتیب ماتریس غیرتکین ماتریسی است که دترمینان آن صفر نیست و بنابراین قابل معکوس کردن است.

ماتریس غیرتکین (غیرمنفرد) در جبر خطی کاربرد زیادی دارد. فرض کنید A یک ماتریس n×n باشد. ماتریس A غیرمنفرد است، اگر تنها جواب معادله Ax=0، جواب صفر x=0 باشد. نمی‌خواهم ذهن شما را با مباحث پیچیده مشوش کنم. در این آموزش شیوه ساده برخورد با خطای Singular matrix را توضیح خواهم داد.

خطای Singular matrix

گاهی برای اجرای الگوریتم حداقل مربعات جزئی خطای Singular matrix مخابره می‌شود. در اینصورت مدل اجرا نمی‌شود و هیچ خروجی نمایش داده نمی‌شود.

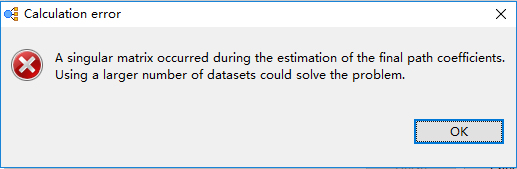
خطای Singular matrix در حداقل مربعات جزئی

سه دلیل اصلی برای این مساله وجود دارد:

یک فیلد داده (پاسخ‌های مربوط به یک گویه) دارای مقداری ثابت باشد.

داده‌های دو فیلد داده (دو گویه مختلف) دارای مقادیر یکسان باشد.

داده‌های یک فیلد داده مضربی از داده‌های یک فیلد دیگر باشد.

روشن است که دلیل اصلی این خطا، به فایل داده برمی‌گردد. اگر داده‌سازی می‌کنید باید به این موضوع توجه کنید که یک فیلد داده تکراری می‌تواند به سادگی باعث شود تا مدل شما اجرا نشود. گاهی نیز دانشحویان داده‌های واقعی گردآوری می‌کنند اما این مشکل همچنان وجود دارد. دلیل این امر نیز آن است که ممکن است برخی پاسخ‌دهندگان فقط یک گزینه مثلا «خیلی‌کم» را برای تمامی پرسش‌ها تیک بزنند. این اتفاق خیلی زیاد رخ می‌دهد و برخی پاسخ‌دهندگان واقعا حوصله جواب دادن به تمامی پرسش‌ها را ندارند.

برای حل مشکل فایل داده را در اکسل باز کنید. میانگین مقادیر همه ستون‌ها را حساب کنید و اگر دو ستون میانگین مشابه داشتند باید اقدام به دستکاری یا تغییرات ساده‌ای در آنها کنید. به این ترتیب به سادگی مشکل ماتریس تکین حل خواهد شد.

جمع‌بندی بحث ماتریس تکین

ماتریس تکین یکی از خطاهای رایج در هنگام انجام روش حداقل مربعات جزئی و مدل‌یابی معادلات ساختاری است. این مساله به فایل داده برمی‌گردد و بخاطر وجود فیلدهای تکراری یا فیلدهایی با مقادیر یکسان رخ می‌دهد. برای حل مشکل به سادگی با نرم‌افزار اکسل فایل داده را باز کنید و مقادیر تکراری یا مشابه را یا حذف کنید یا دستکاری نمایید. اکنون فایل داده را فراخوانی کنید خواهید دید که مدل بدون هیچ مشکلی اجرا خواهد شد.

منبع: حبیبی، آرش؛ جلال‌نیا، راحله. (۱۴۰۱). کتاب حداقل مربعات جزئی. تهران: نارون.