ناواریانسی اندازهگیری
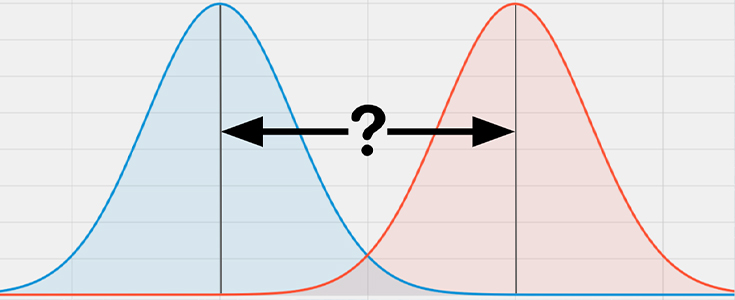
ناواریانسی اندازهگیری (Measurement invariance) برابری واریانس و پراکندگی دادههای گردآوری شده برای یک سازه را در چند گروه بررسی میکند. این روش به همارزی اندازهگیری نیز موسوم است و برای اطمینان از یکسان بودن واریانس دادهها استفاده میشود.
برای نمونه در آزمون تی-مستقل فرض برابری واریانس یک مساله اصلی است که با آزمون لوین بررسی میشود. در تحلیل حداقل مربعات جزئی چند گروهی (PLS-MGA) نیز باید برابری واریانس بررسی شود. سازوکار بررسی پراکندگی دادهها در حداقل مربعات جزئی با پیچیدگی زیادی همراه است. بویژه که این آزمون در حداقل مربعات جزئی با فرض ناواریانسی صورت میگیرد. در این آموزش کوشش بر آن است تا ناواریانسی اندازهگیری تشریح شود.
ناواریانسی اندازهگیری در حداقل مربعات جزئی
در یک تحلیل چندگروهی با روش حداقل مربعات جزئی مساله هنگام مقایسه ضرایب مسیر در میان گروهها، اطمینان از برابری واریانس است. در اینجا باید اطمینان حاصل شود که گویههای سازه در میان گروهها، ناواریانس هستند. برای این منظور استین کمپ و بوگارتنر (۱۹۹۸) رویهای را ارائه کردند که مورد پذیرش جوامع علمی قرار دارد. این روش نشان میدهد که ناواریانسی به اثر تعدیلکننده رستهای برای ضرایب مسیر محدود شده است و در برگیرنده تفاوتهای مرتبط با گروه در مدلهای اندازهگیری نیست.
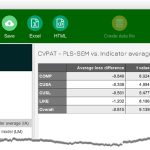
پس از آنکه برآوردها انجام شد در خروجی از Final results گزینه Path Coefficint را انتخاب کنید و سپس در زبانههای موجود PLS-MGA را انتخاب کنید. به این ترتیب میتوانید معناداری اختلاف ضرایب در گروهها را مشاهده کنید. چنانچه مقدار معناداری از سطح خطا کوچکتر باشد اختلاف مشاهده شده میان گروهها معنادار است. همچنین میزان تفاوت ضرایب مسیر میان سازهها براساس دو گروه زنان و مردان نمایش داده میشود. این تحلیل میتواند برای بیش از دو گروه نیز استفاده شود. برای نمونه مشتریان براساس سن، تحصیلات، سابقه خرید و مواردی از این دست به بیش از دو گروه تقسیم میشوند. سازوکار معرفی گروهها و تفسیر نتایج یکسان است.
خلاصه و جمعبندی
در بسیاری موارد بویژه در مطالعات علوم اجتماعی، فرض ناوریانسی اندازهگیری چالشی و پرسشبرانگیز است و گاهی حتی نامعقول بهنظر میرسد. برای همین پژوهشگران باید اثرات عضویت گروه بر برآوردهای مدل اندازهگیری و ساختاری را برای نمونه مدنظر قرار دهند. در دیدگاهی دیگر اعتقاد بر آن است که حداقل مربعات جزئی یک روش مبتنی بر تقریب است و برای موقعیتهایی با پایههای نظری کمتر استوار، طراحی گردیده است. بنابراین بهترین راهکار، بیان احتیاط در تفسیر نتایج تحلیل مسیر شامل گروههای چندگانه است.
منبع: حبیبی، آرش؛ جلالنیا، راحله. (۱۴۰۱). حداقل مربعات جزئی. تهران: نارون.
آمار کاربردی مدیریت | ۰۴ اردیبهشت ۰۲