منطق خاکستری (Grey Logic) روشی برای تصمیمگیری در شرایط دادههای ناقص و نامطمئن است که میان قطعیت کامل و نادانی مطلق تعادل برقرار میکند. این رویکرد برای تصمیمگیری در شرایط ابهام و عدم قطعیت بهکار میرود.
مبانی نظری و تعریف منطق خاکستری
منطق خاکستری رویکردی است که میان دو قطب مطلق درست و نادرست، طیفی از درستیهای نسبی را میپذیرد. این مفهوم ندر آثار دنگ جولانگ (۱۹۸۲) بهصورت نظریهای مستقل تحت عنوان «نظریه سیستم خاکستری» تکامل یافت.
در این نظریه، سیستمها نه کاملاً شناختهشده (سفید) و نه کاملاً ناشناخته (سیاه)، بلکه در منطقهای خاکستری قرار دارند؛ جایی که دادهها ناقص، ناپایدار یا نامطمئناند. نظریه خاکستری یکی از روشهایی است که برای مطالعه عدم اطمینان و ناکامل بودن اطلاعات به کار میرود و استفاده از آن در تحلیل ریاضی سیستمهای با اطلاعات ناقص، روند رو به رشدی را دارد.
در این رویکرد، اطلاعات با درجهٔ خاکستری (ξ\xiξ) بیان میشوند که نشاندهندهٔ میزان قطعی یا ناقص بودن داده است. این تئوری روشی بسیار موثر در مواجهه با مشکلات عدم اطمینان همراه با اطلاعات ناشناخته و ناکامل است.
سیستم خاکستری (Grey system)
سیستم خاکستری به سامانههایی اشاره دارد که بخشی از اطلاعات آنها شناختهشده و بخشی دیگر ناشناخته یا ناقص است. در چنین سیستمهایی، نه میتوان با قطعیت کامل قضاوت کرد (سیستم سفید) و نه با نادانی مطلق روبهرو بود (سیستم سیاه)؛ بلکه دادهها در محدودهای میان این دو حالت قرار دارند.
اگر اطلاعات واضح و شفاف یک سیستم را بارنگ سفید و اطلاعات کاملاً ناشناخته یک سیستم با رنگ سیاه تجسم شود، در این صورت اطلاعات مربوط به بیشتر سیستمهای موجود در طبیعت اطلاعات سفید (کاملاً شناخته شده) و یا سیاه (کاملا ناشناخته) نیستند بلکه مخلوطی از آن دو یعنی به رنگ خاکستری هستند.
این گونه سیستمها را سیستمهای خاکستری مینامند که اصلی ترین مشخصه آن ها، کامل نبودن اطلاعات مربوط به آن سیستم است. این نظریه با ابزارهایی چون «تحلیل رابطه خاکستری» امکان تحلیل روابط میان دادههای ناقص را فراهم میکند.
اعداد خاکستری
هر سیستم خاکستری به وسیله اعداد خاکستری، معادلات خاکستری و ماتریسهای خاکستری توصیف میشود که در این میان اعداد خاکستری به مثابه اتمها و سلولهای این سیستم هستند. عدد خاکستری میتواند به عنوان عددی با اطلاعات نامطمئن تعریف شود. مثلاً رتبه معیارها در یک تصمیمگیری، به صورت متغیرهای زبانی بیان میشوند که میتوان آنها را با بازههای عددی بیان نمود.
یک عدد خاکستری میتواند به صورت زیر تعریف شود:
G ∈ [L , U]
اگر دو عدد خاکستری زیر مفروض باشد در اینصورت داریم:
G۱=[L۱ , U۱]
G۲=[L۲ , U۲]
عملیات جبری روی اعداد خاکستری به صورت زیر است:

عملیات جبری اعداد خاکستری
این بازههای عددی شامل اطلاعات نامطمئن خواهد بود. به عبارت دیگر عدد خاکستری به عددی اطلاق میشود که مقدار دقیق آن نامشخص است اما بازهای که مقدار آن را در بر میگیرد شناخته شده است
طیف خاکستری
به منظور سهولت کار، عبارات کلامی و توابع عضویت متناظر با آنها از مطالعات گذشته استخراج و بنا به نیاز تحقیق مورد تعدیل قرار میگیرند. در زیر نمونهای از عبارات کلامی را میبیند که در بسیاری از مقالات مورد استفاده قرار گرفته است. همانگونه که مشاهده میشود مقادیر بصورت فاصلهای و خاکستری میباشند.
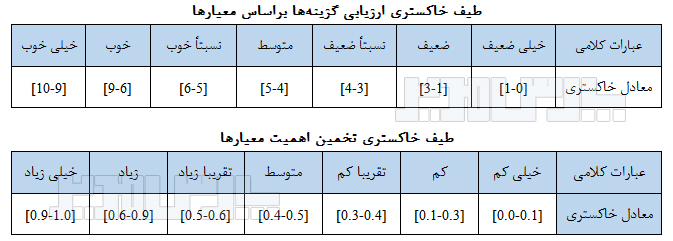
انواع طیف تاپسیس خاکستری (حبیبی، ۱۳۹۷)
دانش را مرزی نیست و همیشه نکاتی برای افزوده هست. آرش حبیبی
انواع مقیاس و طیف اعداد خاکستری
آموزش کامل روش تحلیل خاکستری
آموزش کامل کدنویسی به زبان ساده در اکسل
فایل اکسل کدنویسی شده و open source
مثال عددی و تشریح آن در فایل ورد و حل آن در فایل اکسل
دانلود نرمافزار GRA کدنویسی شده در محیط اکسل
ترجمه کتاب دنگ در زمینه تحلیل خاکستری
زنگ و هوانگ در کتاب تصمیمگیری چندمعیاره در فصل هشت تحلیل رابطه خاکستری براساس رویکرد دنگ را ارائه کرده اند. ترجمه صحیح فارسی فصل هشتم کتاب دنگ در زمینه تحلیل رابطه خاکستری توسط پارس مدیر آماده شده است.
مقایسه منطق فازی و خاکستری
منطق فازی و منطق خاکستری هر دو برای تصمیمگیری در شرایط عدم قطعیت بهکار میروند، اما نوع ابهامی که بررسی میکنند متفاوت است. فازی بر ابهام مفهومی تمرکز دارد، در حالیکه خاکستری به ابهام ناشی از کمبود داده میپردازد.
- در منطق فازی دادهها کامل ولی تعبیرشان نادقیق است.
- در منطق خاکستری بخشی از دادهها وجود ندارد یا ناقص است.
- فازی بر پایهٔ «درجهٔ عضویت» عمل میکند، خاکستری بر پایه «درجه شناخت».
- فازی در کنترل سیستمها رایج است، خاکستری در تحلیل دادههای ناقص.
در نتیجه، منطق فازی بیشتر ابزار تبیین نرمی مفاهیم است، در حالیکه منطق خاکستری ابزاری برای تصمیمگیری علمی در نبود اطلاعات کامل محسوب میشود.
سخن پایانی
منطق خاکستری رویکردی میانافزا میان منطق کلاسیک و فازی است که با پذیرش ناپیوستگی و نقص دادهها، امکان تحلیل و تصمیمگیری دقیقتری را در محیطهای واقعی فراهم میکند. در جهانی که اطلاعات همواره ناقص و متغیرند، تفکر خاکستری نهتنها ضرورت علمی بلکه مهارتی مدیریتی است. این روش به مدیران و پژوهشگران اجازه میدهد حتی با دادههای محدود، مدلهای تصمیمگیری علمی و واقعبینانه بسازند.
منبع: حبیبی، آرش. (۱۳۹۷). کاربرد تئوری خاکستری در مدیریت بازاریابی. بازاریابی پارس مدیر، ۴ (۱۲)، ۳۷-۵۱.