اثر غیرخطی (درجه دوم)
اثر غیرخطی (Quadratic effect) یک مفهوم آماری در معادلات رگرسیونی است که در آن یک عامل با خودش تعامل دارد. بنابراین، X یک عبارت خطی، XY یک برهمکنش با Y و X2 یک اثر غیرخطی (درجه دوم) است.
مفهوم‌سازی‌های استاندارد که زیربنای روابط علت و معلولی در مدل‌های مسیر PLS هستند، به این معناست که سازه‌ها به صورت خطی برهم تأثیر می‌گذارند. با این حال، در برخی موارد، این فرض در این که روابط ممکن است غیرخطی باشند، صادق نیست. این مفهوم با عنوان اثر غیرخطی شناخته می‌شود و با استفاده از نرم‌افزار Smart PLS قابل محاسبه است. در این آموزش با اثر درجه دو شیوه محاسبه آن در حداقل مربعات جزئی آشنا خواهید شد.
اثر غیرخطی در حداقل مربعات جزئی
در رویکرد PLS-SEM، روابط بین سازه‌ها می‌تواند شکل‌های گوناگونی داشته باشد. روابط خطی را می‌توان با خطوط مستقیم (با شیب‌های مثبت یا منفی) هنگام ترسیم مقادیر متغیرهای پنهان در یک نمودار پراکنده نشان داد. روابط غیرخطی شامل همه ارتباط‌هایی است که خطوط مستقیم نیستند بلکه منحنی هستند.
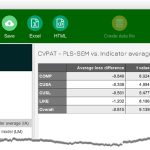
هنگامی که رابطه بین دو سازه غیرخطی است، اندازه اثر بین دو سازه نه تنها به بزرگی تغییر در سازه برونزا بستگی دارد، بلکه به مقدار آن نیز بستگی دارد. در تحلیل اثرات غیرخطی، محققان باید در مورد ماهیت اثر فرضی ایجاد کنند. در حالی که تعداد زیادی از انواع افکت‌های مختلف امکان پذیر است، اثرات درجه دوم رایج ترین هستند. شکل زیر تخمین اثر درجه دوم رضایت بر وفاداری را برای مدل شهرت شرکت در Smart PLS نشان می‌دهد.
اثر غیرخطی در حداقل مربعات جزئی
باسکو و همکاران (۲۰۲۱) و مو و همکاران (۲۰۱۸) تجزیه و تحلیل اثرات درجه دوم و استفاده از آنها در SmartPLS را با جزئیات تشریح کرده‌اند.
سازه وابسته : متغیر وابسته انتخاب شده که یک اثر درجه دوم برای آن تخمین زده می‌شود.
سازه مستقل (متغیر پیش‌بین): فیلدی برای تعریف متغیر پیش‌بین که یک اثر درجه دوم برای آن تخمین زده می‌شود.
شیوه تحلیل اثر غیرخطی (درجه دوم)
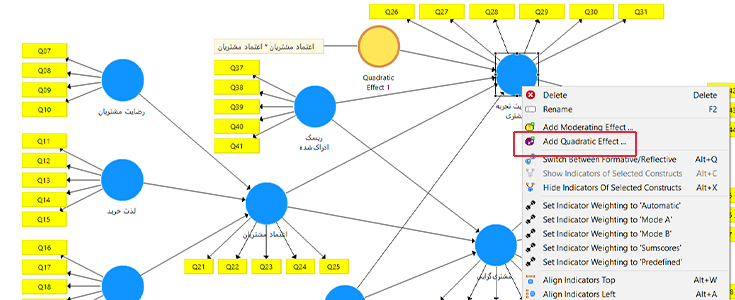
برای محاسبه اثر غیرخطی روی متغیر مورد نظر در نرم‌افزار PLS کلیک راست کنید. سه گزینه وجود دارد:
شاخص محصول (Product Indicator): این رویکرد از تمام ترکیب‌های زوج ممکن از شاخص‌های متغیر پیش‌بینی‌کننده پنهان استفاده می‌کند. این اصطلاحات محصول به عنوان شاخص اصطلاح اثر درجه دوم در مدل ساختاری عمل می‌کنند.
دو مرحله‌ای (Two-stage): این رویکرد از نمرات متغیر پنهان متغیر پیش بینی کننده پنهان از مدل اثرات اصلی (بدون عبارت اثر درجه دوم) استفاده می‌کند. این امتیازات متغیر پنهان ذخیره شده و برای محاسبه شاخص مربع برای تجزیه و تحلیل مرحله دوم استفاده می‌شود که شامل عبارت اثر درجه دوم علاوه بر متغیر پیش بینی می‌شود.
متعامدسازی (Orthogonalization): این رویکرد از باقیمانده‌هایی استفاده می‌کند که با رگرسیون تمام عبارات محصول زوجی ممکن از شاخص‌های متغیر پیش‌بینی‌کننده پنهان (یعنی شاخص‌های محصول) روی همه شاخص‌های پیش‌بینی‌کننده پنهان و متغیر تعدیل‌کننده پنهان محاسبه می‌شوند. این باقیمانده‌ها به عنوان شاخص ترم اثر درجه دوم در مدل ساختاری عمل می‌کنند. باقیمانده‌ها متعامد به همه شاخص‌های متغیر پیش‌بینی‌کننده خواهند بود تا اطمینان حاصل شود که شاخص‌های مدت اثر درجه دوم با هیچ یک از شاخص‌های متغیر پیش‌بینی‌کننده تفاوتی ندارند.
جمع‌بندی و نتیجه‌گیری
در مدل‌های رگرسیونی و حداقل مربعات جزئی می‌توان اثرات غیرخطی متغیرها را نیز محاسبه کرد. نرم‌افزار حداقل مربعات جزئی این امکان را برای پژوهشگران فراهم کرده تا به سادگی اثر غیرخطی (درجه دوم) را محسابه کنند. برای این منظور می‌توان از سه راهکار استفاده کرد که روش مرحله‌ای راهکار بهتری است.
منبع: حبیبی، آرش؛ جلال‌نیا، راحله. (۱۴۰۱). کتاب حداقل مربعات جزئی. تهران: انتشارات نارون.
تهیه و تنظیم: پشتیبانی پارسمدیر
آمار کاربردی مدیریت | ۲۸ بهمن ۰۱
