مدل بازگشتی

مدل بازگشتی (Recursive model) شکل ویژه‌ای از یک مدل معادلات ساختاری است که در آن متغیرهای برون‌زا به صورت همزمان تعیین و تبیین می‌شوند. به بیان دیگر ممکن است در مدل ساختاری متغیرهایی باشد که همزمان با تغییر در متغیر وابسته به صورت غیرمستقیم بر خودشان نیز اثر بگذارند.

از نظر محاسباتی مدل‌های بازگشتی به سادگی مدل‌های غیر بازگشتی نیستند. در بیشتر موارد این امکان وجود دارد که پژوهشگر با مشکل نامشخص بودن برخی از پارامترها مواجه شود، بویژه اگر مدل از پیچیدگی برخوردار باشد. با این وجود در بسیاری مسائل مدیریت و علوم اجتماعی ماهیت مساله به گونه‌ای است که حالت بازگشتی دارد. دشواری محاسبات و کاربردی بودن این نوع الگو هر پژوهشگری را دچار تعارض می‌کند.

در واقع در مدل‌های ساختاری گاهی ما شاهد اثرات متقابل یا دو سویه هستیم و پژوهشگران نشان داده اند که چنین مفروضه هایی به لحاظ روش پژوهش امکان پذیر است. اما باید دید از لحاظ نرم‌افزاری دوستانی که در کلاس‌های ایموس آکادمی شرکت نموده اند در مواجهه با چنین روابط بازگشتی چگونه باید عمل کنند. با توجه به اینکه اثر یک متغیر بر خودش تنها با استفاده از داده‌های ناشی از مطالعات طولی قابل بررسی است، استفاده از داده‌های مقطعی برای چنین اثراتی نیز به طور ضمنی به معنای آن است که یک وضعیت پویا را به یک وضعیت ایستا تقلیل داده ایم. با این حال برخی پژوهشگران نشان داده اند که چگونه با برقرار بودن برخی مفروضه ها، چنین امری امکان پذیر است.

تعریف مدل‌های بازگشتی

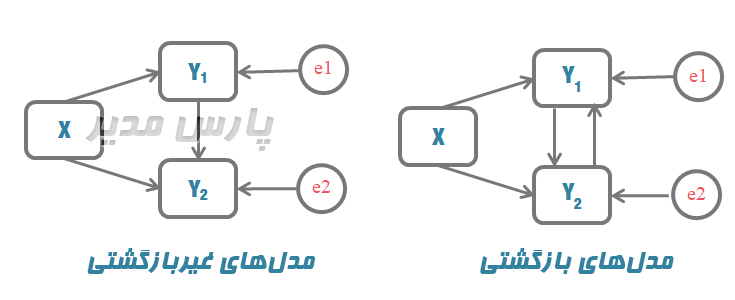
در تدوین مدل‌های ساختاری گاهی وضعیتی پیش می‌آید که در آن پژوهشگر ممکن است بین دو متغیر اثر متقابل یا دو سویه تعریف کند. به این معنی که مایل نیست ارتباط بین دو متغیر را به عنوان یک همبستگی صرف تعریف کند؛ به عبارت دیگر اثر گذاری به صورت یک سویه و تنها از یک متغیر مستقل به سمت متغیر وابسته نیست. مدل‌های بازگشتی را به عنوان مدل هایی تعریف می‌کنند که در آن حلقه ی بازخورد یا پس خورانی (Feedback Loop) وجود دارد. رابطه دو طرفه یا بازگشتی به این معناست که یک متغیر به طور غیرمستقیم برخود اثر می‌گذارد.

در ترسیم این نوع مدل‌ها در ایموس باید دو پیکان رسم نمایند. یعنی یک پیکان یک طرفه از سمت متغیر اول به دوم و بعد یک پیکان یک طرفه هم از سمت متغیر دوم به اول. خوب تا اینجای کار بدون ایراد جلو می‌رود اما نکته مهم اینجاست که در مدل‌های بازگشتی با این تاثیر‌های متقابل، به طور ضمنی خطاهای هر متغیر(هر متغیر وابسته یک خطای باقی مانده دارد. پس در اینگونه مدل ها، هر دو متغیر دارای خطا هستند زیرا هر دو هم زمان هم مستقل و هم وابسته هستند) با یکدیگر همبسته هستند. چرا که وقتی دو متغیر بر هم تاثیر متقابل گذارند بدیهی است که متغیر‌های باقی مانده ی در نظر گرفته نشده در مدل، که در کلاس‌ها خطای باقی مانده خوانده می‌شد باید با هم همبستگی داشته باشند. بنابراین مدل را بدرستی ترسیم و اجرا می‌کنیم.

مثال کاربردی

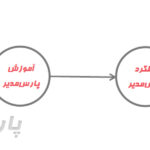
به عنوان مثال با توجه به دو متغیر اعتماد و ریسک ادراک‌شده می‌توان مدلی را تعریف کرد که در آن از یک سو ریسک ادراک‌شده تابعی از اعتماد مشتریان است واز طرف دیگر اعتماد مشتریان نیز تابعی از ریسک ادراک‌شده تعریف می‌شود.

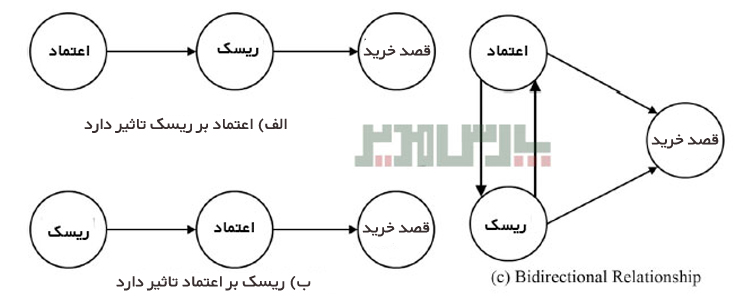
رابطه بازگشتی و غیربازگشتی اعتماد و ریسک ادراک‌شده

به عبارت دیگر در طول زمان نه تنها بالا رفتن اعتماد در میان مشتریان می‌تواند به کاهش ریسک منجر شود، از طرف دیگر بالا رفتن ریسک بین گروهی از افراد خود می‌تواند به کاهش اعتماد در میان آنان منجر شود. در این وضعیت دو پارامتر بتا به عنوان پارامتر آزاد تعریف شده و از درجات آزادی مدل کاسته خواهد شد. چنین وضعیتی را با نام اثر بر خود (Effect on Self) نامگذاری کرده است. اغلب بیش از یک شیوه برای روابط بازخوردی در مدل وجود دارد. ساده ترین شکل آن مدلی است که در آن دو متغیر بدون واسطه بر خودشان اثر می‌گذارند.

تکته نهایی اینکه کلاین معتقد است اتفاقا مدل‌های بازگشتی به جهان واقعی نزدیک تر هستند چرا که بسیاری از متغیر‌های جهان بر یکدیگر تاثیر متقابل و دو سویه دارند اما در نهایت به دلیل اینکه اطلاعات و مشاهدات چنین مدل هایی را باید از مطالعات پیمایشی طولی بدست آورد و همچنین بدلیل اینکه ممکن است تعداد مجهولات معادله ساختاری از تعداد معادلات آن بیشتر باشد و این باعث غیر مشخص شدن پارامتر‌های مدل شود پژوهشگران تمایلی به استفاده از چنین مدل هایی را ندارند.

حلقه بازخورد  در مدل بازگشتی

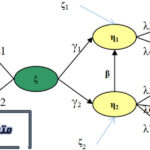
در حالتی کمی پیچیده تر اثر متقابل دو متغیر بر یکدیگر با یک واسطه و همچنین اثر یک متغیر بر خودش با دو واسطه شکل می‌گیرد: وجود حلقه بازخوردی به طور ضمنی به معنای آن است که متغیرهای خطای درگیر در مدل با یکدیگر همبسته اند. به بیان دیگر اگر دو متغیر با یکدیگر تعامل دارند بنابراین منطقی است که عوامل تأثیر گذار بر آن‌ها که در متغیرهای گنجانده شده در مدل ساختاری به عنوان متغیر بیرونی یا درونی آورده نشده اند (یا همان متغیرهای خطا) با یکدیگر همبسته باشند.

به منظور برآورد پارامترهای مدل نوعی از رویکرد حداقل مربعات به نام حداقل مربعات دو مرحله‌ای وجود دارد که به منظور برآورد مدل‌های بازگشتی به کار برده می‌شود. البته برآورد پارامترها در این مدل‌ها با استفاده از روش درستنمایی ماکزیمم نیز امکان پذیر است.

با توجه به اینکه طرح‌های مقطعی تنها یک تصویر منفرد از یک فرآیند پویای در حال حرکت هستند، بنابراین برآورد اثرات دو سویه با داده‌های مقطعی نیازمند برقرار بودن فرضیه تعادل است. فرضیه تعادل به این معنا است که برآورد پارامترها وابسته به زمان خاص گردآوری داده‌ها نیست.  به منظور بررسی این فرضیه وقتی که یک مدل بازگشتی تحلیل و برآورد می‌شود شاخصی به نام شاخص ثبات نیز در خروجی Amos ارائه می‌گردد. به لحاظ کاربردی تفسیر استاندارد شاخص ثبات چنین است که اگر مقدار آن کمتر از ۱ باشد حاکی از برقراری فرضیه تعادل است در حالیکه مقادیر بالاتر از ۱ فقدان برقراری فرضیه تعادل را تأیید می‌کنند.

نتیجه‌گیری

در واقع مدل‌های بازگشتی که بیانگر اثر یک متغیر بر خودش می‌باشد مناسب داده‌های طولی و طرح‌های پانل است که در آن‌ها داده‌ها برای متغیرهای مشابه در دو زمان مختلف گردآوری شده اند، اما با این وجود می‌توان آن‌ها را برای داده‌های مقطعی که در یک زمان جمع آوری شده اند نیز مورد استفاده قرار داد. به عنوان مثال اگر صرفا بر دو متغیر رضایت و اعتماد مشتریان تمرکز کنیم با فرض این که در دو سال متفاوت با ابزارهای یکسان و جامعه آماری یکسان، داده‌های مورد نظر را گردآوری کنیم، مدل مورد نظر ما یک مدل غیر بازگشتی خواهد بود.

بنابراین طرح حلقه‌های بازگشتی ناشی از وجود اثرات متقابل در طول زمان است که امکان آن در یک مدل غیربازگشتی با داده‌های طولی وجود دارد و استفاده از داده‌های غیربازگشتی در واقع برای بررسی آن است. با وجود اهمیت استفاده از مدل‌های بازگشتی در بسیاری از مطالعات اجتماعی، به دلیل مشکلاتی که انجام مطالعات طولی در بر دارد و همچنین به دلیل غیرمشخص شدن برخی از پارامترها در مدل‌های بازگشتی و به تبع آن عدم امکان برآورد پارامترها، بازسازی ماتریس واریانس-کواریانس و محاسبه شاخص‌های برازش مدل، پژوهشگران کمتر تمایل به بهره‌گیری از این نوع مدل‌ها دارند.

منبع: حبیبی، آرش؛ کلاهی، بهاره. (۱۴۰۱). مدل‌یابی معادلات ساختاری و تحلیل عاملی. تهران: جهاد دانشگاهی، چاپ دوم.