همبستگی اسپیرمن (Spearman correlation) یک روش مبتنی بر آمار ناپارامتریک است که شدت و جهت رابطه دو متغیر را نشان میدهد. این روش در موقعیتهایی اهمیت مییابد که رابطهٔ میان متغیرها الزاماً خطی نیست، اما روندی یکنوا (افزایشی یا کاهشی) دارد. در مقاله حاضر روش «همبستگی اسپیرمن» مفهومسازی و آموزش داده خواهد شد.
آشنایی با همبستگی اسپیرمن
شاخص اسپیرمن یک ضریب رتبهمحور و ناپارامتریک است که شدت و جهت رابطهٔ یکنوا میان دو متغیر را بر پایهٔ رتبهها میسنجد. این روش زمانی مناسب است که دادهها رتبهای باشند، توزیع نرمال رعایت نشود، یا مقادیر حدی و ناهموار ساختار داده را دچار بینظمی کرده باشند. مقدار این ضریب بین ۱+ تا ۱– تغییر میکند و بر اساس تفاوت رتبههای دو متغیر محاسبه میشود.
اسپیرمن رابطهٔ یکنوا میان متغیرها را از دریچهٔ رتبهها میسنجد؛ روشی انعطافپذیر و مقاوم که در برابر دادههای نامتقارن و مقادیر افراطی پایداری بیشتری نشان میدهد.
این روش نیز مانند سایر روشهای همبستگی روابط متغیرها را دو به دو در نظر میگیرد. یعنی چنانچه رابطه دو متغیر A و B را با حضور یا بدون حضور متغیری مانند C بسنجید همچنان میزان این رابطه یکسان بدست میآید.
این روش توسط چارلز اسپیرمن ابداع شد و مبتنی بر مفروضات آمار پارامتریک نیست. به عبارت دیگر در این روش برخلاف روش همبستگی پیرسون نیازی به نرمال بودن داده ها نیست.
تحلیل آماری پایاننامه و رساله دکتری
راهنمای تحلیل آماری پایاننامه و رساله دکتری مدیریت:
- تحلیل دادههای آماری با روشهای کمی
- تحلیل و کدگذاری مصاحبه با روشهای کیفی
- تحلیل آماری پایاننامه کارشناسی ارشد
- تجزیهوتحلیل روشهای آمیخته رساله دکتری

برآورد همبستگی اسپیرمن در SPSS
از منوی SPSS از Analyze قسمت Correlate و سپس Bivariate را انتخاب کنید.
در کادر زیر، گزینه Spearman را تیک بزنید.
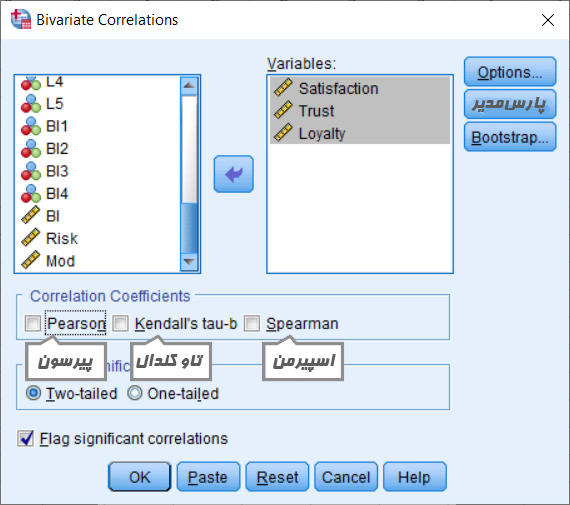
انواع همبستگی دومتغیری
متغیرهایی که میخواهید همبستگی آنها را محاسبه کنید بوسیله دکمه ⇐ به کادر Variables منتقل کنید.
اگر میخواهید نتایج معنادار با ستاره مشخص شود تیک Flag significant correlations را فعال کنید.
روی دکمه OK کلیک کنید تا نتایج ظاهر شود.
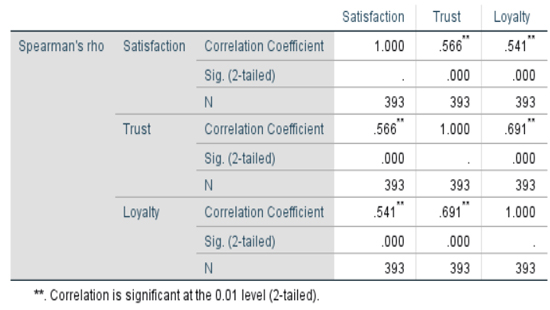
نتایج ضریب همبستگی اسپیرمن
نتایج آزمون همبستگی اسپیرمن نشان میدهد:
ضریب اسپیرمن رابطه بین رضایت و اعتماد ۰/۵۶۶ و مقدار معناداری نیز ۰/۰۰۰ برآورد شد. بنابراین رضایت و اعتماد رابطه مثبت و معناداری دارند.
رابطه بین رضایت و وفاداری نیز ۰/۵۴۱ و اعتماد و وفاداری نیز ۰/۶۹۱ بدست آمد.
اگر با روش پیرسون نیز این آزمون را انجام دهید نتایج تا میزان زیادی مشابه برآورد خواهد شد.
سخن پایانی
در پایان باید گفت اسپیرمن ابزاری ضروری برای پژوهشگرانی است که با دادههای رتبهای، نمونههای کوچک، توزیعهای نامتقارن یا الگوهای یکنوا سروکار دارند. این شاخص محدودیتهای روشهای خطی را جبران میکند و در شرایطی که پیرسون کارایی خود را از دست میدهد، تصویری دقیقتر و قابل اتکاتر از رابطهٔ میان متغیرها ارائه میدهد. انتخاب درست میان روشهای رتبهای و خطی، بهجای تکیه بر عادت، کیفیت تحلیل را ارتقا میدهد و مسیر پژوهش را روشنتر میسازد.
منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: ناروندانش.
سوالات متداول
این ضریب برای دادههای رتبهای، دادههای کمّی غیرنرمال، یا زمانی که رابطهٔ میان متغیرها خطی نیست اما روند یکنوا دارد بهکار میرود. چون اسپیرمن دادهها را رتبهگذاری میکند، برای تحلیل روابطی که در سطح مقادیر مشاهدهای قابل اتکا نیستند، گزینهٔ ایمنتری بهشمار میآید.
تا حد زیادی بله. چون رتبهها مبنای محاسبه هستند، دادهٔ پرت فقط رتبهٔ خود را تغییر میدهد و اثرش بر ساختار کلی رتبهبندی ناچیز است. به همین دلیل اسپیرمن برای دادههایی که پراکندگی نامتقارن یا مقادیر افراطی دارند، برتری محسوسی دارد.
خیر. هر نوع دادهٔ رتبهای مناسب است و حتی دادههای فاصلهای/نسبتی نیز میتوانند با رتبهگذاری وارد تحلیل شوند. این ویژگی موجب شده اسپیرمن یک گزینهٔ ناپارامتریک و انعطافپذیر باشد که در شرایط نامطمئن یا دادههای آشفته عملکرد خوبی دارد.
بله، اما شدت رابطه بر اساس فاصلهٔ رتبهها سنجیده میشود نه مقادیر واقعی. بنابراین اگرچه بازهٔ عددی مشابه (۱ تا ۱–) دارد، تفسیر آن در سطح ترتیبی است. مثلاً اگر rs=0.80 باشد یعنی هرچه یک متغیر رتبهٔ بالاتری بگیرد، دیگری نیز معمولاً رتبهٔ بالاتری کسب میکند.
خیر. اسپیرمن فقط روابطی را بهخوبی ثبت میکند که بهطور پیوسته افزایشی یا کاهشی باشند. هنگامی که رابطه فراز و فرود داشته باشد (مثلاً ابتدا زیاد شود، بعد کم شود)، این روش بخش زیادی از اطلاعات را از دست میدهد و مقدار ضریب کوچک میشود، درحالیکه رابطهٔ واقعی پیچیدهتر است.