آمار توصیفی

موضوع آمار توصیفی (Descriptive statistics) تنظیم و طبقهبندی دادهها، نمایش ترسیمی، و محاسبهٔ مقادیری از قبیل نما، میانگین، میانه و … میباشد. این حوزه آماری، حاکی از مشخصات یکایک اعضای جامعهٔ مورد بحث است. در آمار توصیفی اطلاعات حاصل از یک گروه، همان گروه را توصیف میکند و اطلاعات به دست آمده به دستهجات مشابه تعمیم داده نمیشود. به طور کلی از سه روش در آمار توصیفی برای خلاصهسازی دادهها استفاده میشود: استفاده از جداول، استفاده از نمودار و محاسبه مقادیری خاص که نشاندهنده خصوصیات مهمی از دادهها باشند.
به طور کلی، روشهایی را که به وسیله آنها میتوان اطلاعات گردآوری شده را تنظیم کرده و خلاصه نمود، آمار توصیفی مینامیم و در یک کلام آمار توصیفی عبارت از مجموعه روشهایی است که پردازش دادهها را فراهم میسازد. آمار توصیفی مبتنی بر دیدگاه آمار کاربردی مدیریت تشریح شده است.
برای اینکه نتایج مناسب و مطلوب از اطلاعات که در آمار گیریها جمع آوری میکنیم، به دست آید باید:
- اعداد نماینده واقعی مشاهدات بوده و غیرواقع یا غلط نباشند
- به نحو مفیدی تهیه و تنظیم شوند
- به نحو صحیح تجزیه و تحلیل گردند
- قابل نتیجهگیری صحیح باشند
آمار توصیفی با کمک نرمافزار SPSS
محاسبات مربوط به انواع شاخصهای آمار توصیفی را در منوی Analyze زیرمنوی Descritive Statistics خواهید یافت. فراوانیها، شاخصهای توصیفی، جداول متقاطع و انواع نسبتها در این قسمت قابل دسترسی است. سه فرمان Frequencies, Descriptives و Crosstabs در کتاب SPSS پارس مدیر بررسی شده است. بطور کلی بخاطر داشته باشید برای بدست آوردن انواع فراوانی مراحل زیر را انجام دهید:
از منوی Analyze زیرمنوی Descritive Statistics و سپس Frequencies را انتخاب کنید.
متغیرهای مورد نظر را به کمک فلش به باکس Variables منتقل کنید.
دکمه Stattistics را بزنید تا کادر جدیدی باز شود.
میانگین، میانه، مد، انحراف معیار و هر آماره توصیف دلخواه دیگری که نیاز دارید را فعال کنید.
در پایان هر دو کادر را تایید کنید تا همه نوع خروجی توصیفی را در مشت داشته باشید.
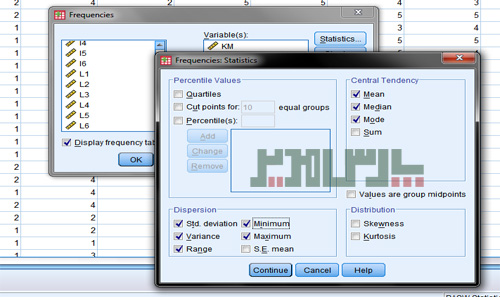
آمار توصیفی در SPSS
پاورپوینت آموزش کامل آمار توصیفی
اهمیت آمار توصیفی در آمار بر هیچکس پوشیده نیست. به همین منظور اسلاید آموزشی در زمینه آمار توصیفی تهیه شده که به طور کامل مفاهیم آمار توصیفی را بیان میکند. برای دانلود این فایل آموزشی به انتهای این مطلب مراجعه کنید. این آموزش شامل سرفصلهای زیر است :
برای ورود به بحث آمار توصیفی ابتدا جامعه و نمونه تشریح شده است. سپس انواع متغیرهای پژوهش و انواع مقیاس اندازهگیری متغیرها بیان شده است.
جدولهای فراوانی آماری
- فراوانی
- فراوانی نسبی
- فراوانی تجمعی
- فراوانی نسبی تجمعی
اطلاعات بدست آمده از یک تحقیق غالباً تودهای از اطلاعات خام، بی معنی و بدون نظم هستند که هر نوع نتیجهگیری و تفسیر آنها غیر ممکن است. بنابراین برای هر نوع تجزیه و تحلیل اطلاعات لازم است دادهها (بخصوص دادههایی که در سطح مقیاساندازهگیری فاصلهای و نسبی به دست آمدهاند) براساس یک نظم منطقی طبقه بندی (Classification) شوند تا به صورت معنیدار و قابل تفسیر در آید. طبقه بندی دادهها مستلزم محاسبه مرحله به مرحله دامنه تغییرات، تعداد طبقات، فاصله طبقات، انواع فراوانیها با استفاده از فرمولهای مشخص است. طبقه بندی دادهها تمام اطلاعات در یک جدول به نام جدول توزیع فراوانی (Frequeny Table) گردآوری میشود.
فراوانی: در دادههای آماری دسته بندی نشده به تعداد دفعاتی که هر داده تکرار میشود فراوانی مطلق آن داده گفته میشود و آن را با fi نشان میدهند.
فراوانی نسبی: نسبت فراوانی مطلق هر داده به تعداد کل داده ها، فراوانی نسبی نامیده میشود.
فراوانی تجمعی: اگر فراوانی مربوط به هر دسته را با مجموع فراوانیهای قبل از آن دسته جمع کنیم، فراوانی تجمعی یا تراکمی مربوط به آن دسته به دست میآید.
نمودارهای آماری
- هیستوگرام
- چندبر فراوانی
- چندبر فراوانی تجمعی
- منحنیهای فراوانی
- نمودار شاخه و برگ
معیارهای مرکزی (Dispersion Index)
- میانگین
- میانه
- نما
- چندک ها
مد یا نما: در یک تعریف ساده، نما Mode به دادهای گفته میشود که در یک مجموعه از اعداد بیشتر از همه رخ دهد. برای مثال اگر در یک کلاس هفت نفر ۱۲ ساله باشند، ده نفر ۱۳ ساله باشند و چهار نفر ۱۴ ساله نما ۱۳ است زیرا بیش از هر سن دیگری ۱۳ ساله وجود دارد. در انتخابات به نما معمولا «حداکثر آرا» گفته میشود و نامزدی که بیشترین آرا را کسب کند برنده انتخابات است حتی اگر تعداد آرای او حداکثر (بیشتر از نصف) کل آرا نباشد.
میانه: میانه Median در وسط چند مقدار در یک مجموعه از مقدارها قرار دارد. برای مثال اگر سه دانشآموز در یک آزمون نمرههای ۸۱، ۸۴ و ۹۳ گرفته باشند، مقدار وسط که ۸۴ است به عنوان میانه انتخاب میکنیم.
میانگین: میانگین Mean معمولی یا میانگین حسابی (که گاهی اوقات متوسط نیز نامیده میشود) برابر است با حاصلجمع تمام مقدارها تقسیم بر تعداد مقدارها. برای مثال اگر سه دانشآموز در یک آزمون نمرههای ۸۱، ۸۴ و ۹۳ گرفته باشند، میانگین برابر است با ۸۱ + ۸۴ + ۹۳ / ۳ که میشود ۸۶.
معیارهای پراکندگی (Centrol Index)
- دامنه
- میانگین انحرافها از میانگین
- میانگین انحرافها از میانه
- دامنه چارکی
- دامنه صدکی
- واریانس دادهها
- انحراف معیار
- ضریب تغییرات
انحراف معیار (Standard deviation) مفهومی است که میزان پراکندگی دادههای یک مجموعه را مشخص میکند. بدین جهت یکی از مهمترین مقیاسهای آماری در زمینه آمار توصیفی به حساب میآید. اگر میانگین برآوردی از نقطه ثقل توزیع دادههای یک مجموعه به دست میدهد. از این رو مقیاسی تکبعدی برای برآورد یک مجموعه دادهها فراهم میسازد. میتوان گفت که انحراف معیار نیز میزان پراکندگی دادهها از نقطه میانگین را نشان میدهد. از این رو مقیاسی دوبعدی برای برآورد توزیع دادهها در اختیار ما قرار میدهد. واریانس به صورت «مقدار متوسط مربع اختلاف مقادیر از میانگین» تعریف شده است.
دانلود پاوپوینت آموزش آمار توصیفی
آمار کاربردی مدیریت | ۰۸ فروردین ۹۲





سلام. ممنون از سایت خوبتون.
من در بخش توضیف آماری از سن، جنس، تحصیلات و سابقه کاری برای جامعه آماریم،آمار داده بودم. داور در سرجلسه دفاع پرسید که اگر این موارد در تحقیقاتتان تاثیر گذار هستند؟ اگر آره؛ در مدل مفهومیتون باید قید میشده و اگر نه برای چه در آمار توصیفی بررسی کرده اید؟ من باید چه جوابی می دادم؟ مگر این عوامل در همه تحقیقات بازگو نمی شوند.
برای داوری که این نظر را داده شفای عاجل طلب میکنم. در هر مقاله معتبری از پایگاه ساینس دایرکت و امرالد و اشپرینگر هم ملاحظه کنید قبل از هر بحثی آمار توصیفی جامعه مورد پژوهش ارائه میشود.
سلام. اول از سایت خیلی خیلی کاربردی و عالی که در اختیار دانش پژوهان قرار دادین واقعا سپاسگذارم، به جرات میتونم بگم یکی از بهترین هاست. سوال من اینه روش محاسبه ضریب کندال در پرسشنامه ی دلفی برای محاسبه ی هماهنگی نظرات راجع به مولفه و حذف و تایید آن مشابه همان ضریب کندال معمول در پرسشنامه هاست؟ یا باید برای هر سوال جداگانه ان را به دست آورد؟ آموزش خاصی ندیدم و اولین باره دلفی کار میکنم. فقط برای اطمینان پرسیدم ممنون میشوم اگه راهنمایی کنید.
درود بر شما. لطفا آموزش مربوط به ضریب کندال را مطالعه کنید اگر پاسخ پرسشتان را پیدا نکردید زیر همان مطلب کامنت بگذارید.
سلام،در امار توصیفی جدولی از شاخص های توصیفی برای متغیرها (به ازای سوالات پژوهش) آورده میشه که شامل میانگین،انحراف معیار،کمینه و بیشینه است.هرکدوم از این اعداد چه معنایی دارند و آیا محدوده خاصی دارند؟