بازنمونه‌گیری (Re-sampling)

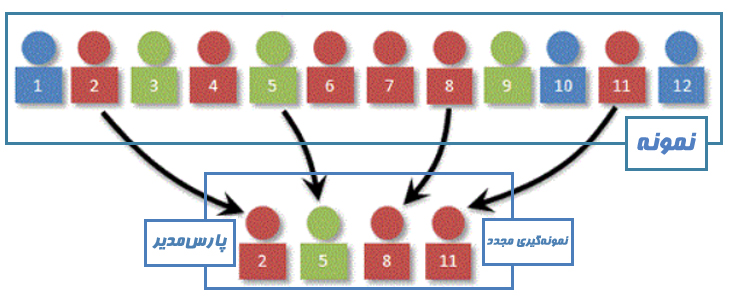
بازنمونه‌گیری (Re-sampling) روشی آماری است که در آن برای کاهش اریبی برآورد از میان نمونه‌های موجود تعدادی نمونه جدید انتخاب می‌شود. به زبان ساده اگر از یک جامعه به حجم N نمونه‌ای به حجم n را انتخاب کرده باشید از میان همان نمونه n تعداد جدیدی به عنوان نمونه انتخاب می‌شوند.

چارچوب آماری یا فهرست واحدهای آمارگیری، اساس و مبنای یک طرح آمارگیری نمونهای را تشکیل می‌دهد. گاهی ممکن است چارچوبی که تمامی واحدهای جامعهی مورد مطالعه را پوشش دهد در دسترس نباشد، اما امکان دستیابی به پوشش کامل، با تلفیقی از دو یا چند چارچوب فراهم شود. در چنین حالتی به منظور دسترسی به پوشش مناسب، از دو چارچوب یا بیش تر به طور همزمان استفاده می‌شود.

گاهی نیز ممکن است یک چارچوب، پوشش کامل را برای جامعهی مورد مطالعه فراهم کند، اما چارچوب ناقص دیگری موجود باشد که هزینه آمارگیری از آن کم تر از هزینه آمارگیری از چارچوب کامل باشد. در این شرایط به دلیل پایینتر بودن هزینه آمارگیری از این چارچوب، می‌توان با هزین‌های مشخص و ثابت از بازنمونه‌گیری استفاده کرده و اندازهی نمونه را بزرگتر و کارایی را افزایش داد. گاهی نیز ممکن است یک چارچوب فهرستی کامل، در دسترس باشد اما عملاً با گذشت زمانی نسبتاً طولانی به دلیل بروز تغییرات فراوان در آن، منبعی برای بروز خطاهای غیر نمونه‌گیری شود. از آنجا که یک فهرست ناحیها‌ی، کم تر در معرض تغییرات می‌باشد، ترکیب آن با یک چارچوب از اعضای جامعه که احتمالاً ناقص باشد، می‌تواند نتایج مفیدی را حاصل نماید. چنین آمارگیری‌هایی تحت عنوان آمارگیری‌های چندچارچوبی به کار میروند.

خطا در برآورد

از آنجایی که به جای استفاده از جامعه آماری، نمونه آماری به کار گرفته شده است، برآورد پارامتر جامعه با خطا همراه است. این خطا از دو دیدگاه بررسی می‌شود. «اُریبی» (Bias) و «خطای نمونه‌گیری» (Sampling Error).

• اُریبی: این خطا به علت تمایل نمونه به یک سمت از جامعه آماری است. این میزان خطا نشان می‌دهد که به طور متوسط برآوردگر با مقدار واقعی چقدر تفاوت دارد.
• خطای نمونه‌گیری: از آنجایی که نمونه به صورت تصادفی از جامعه آماری انتخاب شده است، با انتخاب نمونه دیگر نیز مقدار برای پارامتر جامعه با مقدار دیگری برآورد می‌شود. خطای نمونه‌گیری نشان می‌دهد که واریانس این برآوردگر چقدر است. یعنی اگر چندین بار نمونه‌گیری انجام شود، به طور متوسط پراکندگی این برآوردها چقدر خواهد بود.

در نتیجه باید شیوه نمونه‌گیری به شکلی باشد که این دو خطا در آن کمترین حالت خود را داشته باشند. بنابراین شیوه‌های نمونه‌گیری متنوعی مانند «نمونه‌گیری تصادفی ساده» (Simple Random Sampling)، «نمونه‌گیری سیستماتیک» (Systematic Random Sampling)، «نمونه‌گیری طبقه‌ای» (Stratified Random Sampling) و «نمونه‌گیری خوشه‌ای» (Clustering Sampling) بوجود آمده‌اند تا الگویی صحیح برای انتخاب اعضای نمونه آماری ارائه دهند.

روش‌های بازنمونه‌گیری

با استفاده از نمونه آماری، برآورد پارامتر جامعه امکان پذیر است. ولی این برآورد براساس یک نمونه تصادفی حاصل شده است و دقت آن اندازه‌گیری نشده. یک روش برای مشخص کردن دقت برآوردگر، بازنمونه‌گیری و برآورد پارامتر است. به این ترتیب چندین برآوردگر براساس هر نمونه تولید شده در روش بازنمونه‌گیری حاصل می‌شود و می‌توان واریانس یا دقت این برآوردگرها را محاسبه کرد. در حقیقت بازنمونه‌گیری روشی مقرون به صرفه با استفاده از یک نمونه، برای محاسبه دقت برآوردهای حاصل شده است. روش‌های بازنمونه‌گیری ساده بوده و احتیاج به محاسبات طولانی ندارند.

سری تیلور : اسکینر و رائو روش خطی سازی سری تیلور را پیش نهاد دادند. برای براورد واریانس اینگونه براوردگرها، روشهای مختلفی از جمله خطی سازی سری تیلور پیش نهاد شده است. استفاده از این روش مستلزم محاسبهی مشتقهای جزئی بوده و این محاسبات با افزایش تعداد چارچوبها پیچیدهتر می‌شود.

روش جک نایف: از یک نمونه با حجم n، چندین نمونه با استفاده از حذف یک به یک عناصر تولید شده و برآوردیابی انجام می‌شود. میانگین برآوردگرهای تولید شده می‌تواند به عنوان برآوردگر جدید معرفی شده و خطای آن محاسبه شود.

روش بوت‌استرپ: از یک نمونه با حجم n چندین نمونه با جایگذاری، تهیه می‌شود. از این نمونه‌ها به عنوان مجموعه «داده آموزشی» (Learning Data) استفاده شده و برآورد پارامتر جامعه انجام می‌شود. از مابقی اعضایی که در باز‌نمونه‌گیری به کار نرفته‌اند به عنوان مجموعه «داده‌های آزمایشی» (Test Data) استفاده می‌شود.