نرخ ناسازگاری مقایسه‌های زوجی

نرخ ناسازگاری (Inconsistency Ratio) شاخصی است که نشان می‌دهد چه میزان مقایسه‌های زوجی انجام شده با هم سازگاری دارند. مقایسه‌های زوجی توسط خبرگان صورت می‌گیرد و در صورتی می‌توان به نتایج مقایسه‌ها اعتماد کرد که این مقایسه‌ها سازگار باشند.

اساس تحلیل در روش‌های فرایند تحلیل سلسله‌مراتبی (AHP) و فرایند تحلیل شبکه (ANP) بر مقایسه‌های زوجی توسط خبرگان استوار است. بنابراین هرگونه خطا و ناسازگاری در مقایسه عناصر، نتیجه نهایی به دست آمده از محاسبات را تحت تاثیر قرار می‌دهد.

نرخ سازگاری مقایسه‌ها با یک مثال قابل تشریح است. برای نمونه اگر عنصر A نسبت به B ارزش ترجیحی ۳ داشته باشد و عنصر B نسبت به C ارزش ترجیحی ۲ داشته باشد، آنگاه باید انتظار داشت عنصر A نسبت به C ارزش ترجیحی ۶ داشته باشد. یک نمونه مقایسه سازگار و یک نمونه مقایسه ناسازگار در زیر آمده است:

مقایسه سازگار: الف از ب بهتر است؛ ب از ج بهتر است؛ الف از ج خیلی بهتر است.

مقایسه ناسازگار: الف از ب بهتر است؛ ب از ج بهتر است؛ ج از الف بهتر است.

شاید بررسی سازگاری مقایسه سه عنصر ساده باشد، اما وقتیکه تعداد مقایسه‌ها افزایش یابد اطمینان از سازگاری مقایسه‌ها به سادگی میسر نبوده و از نرخ سازگاری استفاده می‌شود. تجربه نشان داده است که اگر نرخ سازگاری کمتر از ۰/۱ باشد سازگاری مقایسه‌ها قابل قبول است. در غیر اینصورت مقایسه‌ها باید تجدید نظر شود. گام‌های زیر برای محاسبه نرخ سازگاری در تکنیک AHP قطعی و FAHP فازی به کار گرفته می‌شود.

محاسبه نرخ ناسازگاری در فرایند تحلیل سلسله‌مراتبی معمولی

گام ۱ محاسبه بردار مجموع وزنی: ماتریس مقایسه‌ زوجی را در بردار ویژه ضرب کنید. بردار جدیدی را که به این طریق بدست می‌آید، بردار مجموع وزنی نامیده می‌شود.

گام ۲ محاسبه بردار سازگاری: هر عنصر بردار مجموع وزنی را بر عنصر متناظر در بردار ویژه تقسیم کرده، بردار حاصل بردار سازگاری نامیده می‌شود.

گام ۳ برآورد lmax: میانگین عناصر بردار سازگاری lmax را به دست می‌دهد. بیشتر مواقع به جای محاسبه lmax از روش تقریبی میانگین هندسی استفاده می‌شود. پارامتر L مقدار تقریبی lmax است.

گام ۴ محاسبه شاخص سازگاری (CI) : اگر تعداد عناصر جدول مقایسه زوجی n باشد، شاخص سازگاری بصورت زیر تعریف می‌شود:

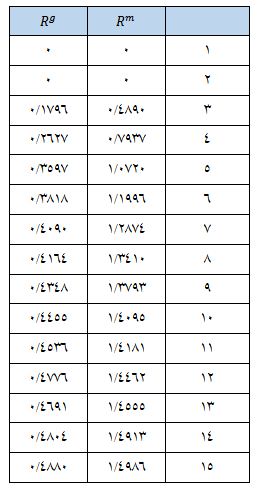
گام ۵ محاسبه شاخص تصادفی: شاخص تصادفی بودن از جدولی مانند جدول ۱ یا جدول ۲  استخراج می‌شود.

شاخص تصادفی بودن

گام ۶ محاسبه نرخ سازگاری: نرخ سازگاری از تقسیم شاخص سازگاری بر شاخص تصادفی بدست می‌آید. اگر نرخ سازگاری ۱/۰ یا کمتر باشد مقایسه‌ها سازگار است.
CR = CI / RI

محاسبه نرخ ناسازگاری در فرایند تحلیل سلسله‌مراتبی فازی FAHP

دو پژوهشگر به نام گاگوس و بوچر (۱۹۹۸) روشی را برای محاسبه درجه سازگاری ماتریس‌های مقایسات زوجی فازی ارائه نموده‌اند. در این روش به منظور بررسی سازگاری، لازم است از هر ماتریس مقایسه زوجی مانند Ã(n*n) به دو ماتریس مجزا افراز می‌شود. علامت مدک یا  ̃   نشانه فازی است.

ماتریس A^m از مقادیر میانی ترجیحات خبرگان تشکیل می‌شود

ماتریس A^g از میانگین کران بالا و پایین TFN تشکیل می‌شود.

شاخص تصادفی بودن گوگوس و بوچر

برای یافتن نرخ سازگاری، بردار وزن هر یک از این دو ماتریس باید محاسبه شود. از آنجا که این ماتریس‌ها شامل داده‌های عددی (غیر فازی) هستند، می‌توان از روش ساعتی برای محاسبه بردار وزن استفاده نمود. بنابراین ابتدا ماتریس مقایسه زوجی فازی به دو ماتریس قطعی افراز می‌شود و سپس به روش ساعتی نرخ ناسازگاری هر ماتریس قطعی شده A^m و A^g محاسبه خواهد شد. تنها تفاوت در اینجا استفاده از شاخص تصادفی است که گاگوس و بوچر پیشنهاد داده‌اند. روشن است در پایان دو نرخ ناسازگاری وجود خواهد داشت که با CR^m و CR^g نمایش داده می‌شود. اگر هر دو روش نرخ ناسازگاری را بالای ۰٫۱ نشان دهد باید با تجدیدنظر در نتایج از خبرگان خواسته شود مجدداً ماتریس‌ها را تکمیل کنند. همچنین حتی اگر یکی از دو مقدار هم از آستانه ۰٫۱ بزرگتر باشد توصیه اکید آن است که مقایسه‌ها از نو انجام شود.

منبع: حبیبی، آرش؛ آفریدی، صنم. (۱۴۰۱). تصمیم‌گیری چندشاخصه، تهران: انتشارات نارون.