درجه عضویت فازی
درجه عضویت فازی (Membership degree) به میزان تعلقپذیری یک عنصر به یک مجموعه فازی اشاره دارد و بین دو مقدار ۰ و ۱ در نوسان است. این مفهوم کلید درک تفاوت مجموعه فازی و مجموعههای کلاسیک است.
در منطق کلاسیک تعلق یا عضویت یک عضو به یک مجموعه مفهومی کاملاً قطعی و دقیق است. بنابراین یک شی یا عضو یک مجموعه است و یا نیست. پس تابع عضویت فقط میتواند دو مقدار ۰ و ۱ را داشته باشد. به منظور توصیف تغییرات تدریجی و اندک لطف علی عسگرزاده درجات بین ۰ و ۱ و مفهوم درجه عضویت یا تابع عضویت را معرفی کرده است. برای این منظور تابع عضویت µ تعریف میشود که همواره مقادیری از بازه [۰و۱] را شامل میشود. یک عدد فازی به وسیله یک بازه از اعداد حقیقی که هر کدام یک درجه عضویت بین ۰ و ۱ را دارند مشخص میشود.
تعریف: مجموعه فازی Ã از مجموعه مرجع U به صورت زوجهای مرتب زیر نشان داده میشود:
à ={( x, μÃ(x) )|x∈U}
تذکر: بطور قراردادی علامت مد ~ بالای حروف لاتین نشان دهنده فازی بودن عنصر یا مجموعه است.
آرش حبیبی
در رابطه بالا x عنصری از مجموعه à است که ویژگی این مجموعه را تا حدودی دارد. حدود یا درجه عضویت با نشان داده میشود. درجه عضویت μÃ(x) نشان میدهد عنصر x تا چه میزان ویژگی مجموعه à را دارد.
درجه عضویت یک عدد فازی مثلثی
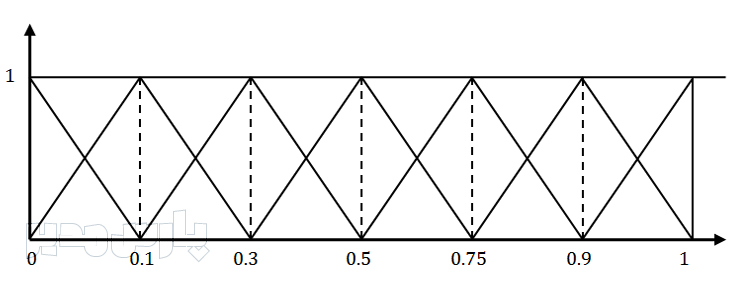
عدد فازی مثلثی (Triangular fuzzy number, TFN) یکی از انواع اعداد فازی است که با سه عدد حقیقی به صورت F=(l,m,u) نمایش داده میشود. کران بالا که با u نشان داده میشود بیشینه مقادیری است که عدد فازی F میتواند اختیار کند. کران پایین که با l نشان داده میشود کمینه مقادیری است که عدد فازی F میتواند اختیار کند. مقدار m محتمل ترین مقدار یک عدد فازی است. تابع عضویت یک عدد فازی مثلثی به صورت زیر است:
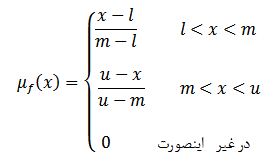
درجه عضویت یک عدد فازی مثلثی
با توجه به تابع عضویت اعداد مثلثی مشخص است اگر x بین l و m باشد آنگاه هر چه بزرگتر باشد درجه عضویت آن نیز بزرگتر خواهد شد تا جائیکه برای x= m درجه عضویت برابر یک میشود. اگر x بین m و u باشد هرچه بزرگتر باشد، درجه عضویت کوچکتر خواهد شد و در x= u درجه عضویت صفر خواهد شد. بنابراین میتوان گفت درجه عضویت x در فاصله [l, m] به صورت یکنواخت افزایشی و در فاصله [m, u] به صورت یکنواخت کاهشی است. اگر l= m= u باشد در اینصورت عدد فازی به یک عدد قطعی تبدیل خواهد شد.
نتیجهگیری
مجموعههای فازی کلید درک منطق فازی هستند و ویژگی اصلی این مجموعهها، درجه عضویت اعضای این مجموعهها است. در یک مجموعه قطعی و آشنا عناصر یا به یک مجموعه تعلق دارند یا به آن تعلق ندارند. اما در مجموعههای فازی هر یک از اعضا با میزانی مشخص بین ۰ تا ۱ به یک به آن مجموعه تعلق دارند. برای نمونه یک نفر با سن ۳۰ سال به میزان ۶۰% عضو مجموعه افراد جوان است و یک فرد با سن ۲۵ سال به میزان ۹۰% عضو مجموعه افراد جوان محسوب میشود. اجازه دهید با این مصرع آموزش را به پایان ببرم: آیا وجود حاضر غائی شنیدهای؟
منبع: حبیبی، آرش؛ آفریدی، صنم. (۱۴۰۱). تصمیمگیری چندشاخصه، تهران: انتشارات نارون.
تصمیم گیری چندمعیاره | ۱۳ آبان ۹۸





خیلی خوب بود ممنون
🙏🙏
سلام
درجه عضویت فازی مثلثی تو نرم افزار متلب محاسبه میشه یا باید اینو دستی محاسبه کنیم
درود بر شما. درجه عضویت بیشتر توسط خود پژوهشگر تعیین میشود.