مجموعه فازی

مجموعه فازی (Fuzzy set) یا مجموعه غیرقطعی شامل دسته‌ای از عناصر است که هر کدام از یک درجه عضویت ویژه در آن مجموعه برخوردار است. در مجموعه‌های قطعی یک عنصر یا عضو یک مجموعه است یا عضو آن نیست اما در مجموعه‌های فازی میزان عضویت اعضا براساس قواعد مشخصی تعیین می‌شود.

درک مفهوم «مجموعه فازی» یا Fuzzy set در کانون یادگیری کاربرد منطق فازی در مدیریت قرار دارد. به دیگر سخن منطق فازی را می‌توان استدلال با مجموعه‌های فازی بیان کرد. مجموعه‌های فازی در قیاس با مجموعه‌های کلاسیک و مفهوم درجه عضویت قابل تشریح است. در یک مجموعه کلاسیک هر یک از اجزا مجموعه دارای درجه عضویت یک بوده و سایر عناصر درجه عضویت صفر دارند. یعنی یک عنصر یا عضوی از مجموعه A است و یا عضو آن نیست. مجموعه‌های فازی برخلاف مجموعه‌های کلاسیک، دارای مرزهای مشخص و خوب تعریف شده‌ای نیست.

مثال برای درک بهتر

برای نمونه یک فرد ۱۵ ساله را در نظر بگیرید. براساس اصول قطعی این فرد یا در مجموعه افراد نوجوان قرار می‌گیرد یا در مجموعه افراد جوان. اما براساس اصول مجموعه‌های فازی این فرد می‌تواند تا حدودی در مجموعه افراد جوان و تا حدودی در مجموعه افراد نوجوان قرار دارد.

برای نمونه دیگر براساس مکتب کلاسیک، دانش آموزی که نمره ۹/۵ می‌گیرد در مجموعه مردود قرار گرفته و دانش‌آموزی که نمره ۱۰ می‌گیرد در مجموعه قبول قرار می‌گیرد. اکنون این پرسش مطرح می‌شود: آیا تفاوت این دو نفر در آن حد است که نفر اول باید یکسان از نفر دوم عقب بماند. اینگونه تعریف از یک ارزش آستانه مطلق برای شمول افراد در یک مجموعه در منطق کلاسیک جای دارد. منطق فازی مفاهیم ضروری جدیدی را در قالب عدم اطمینان و ابهام وارد ریاضیات و منطق کرده و مبانی علم کلاسیک را متحول ساخته است.

تفاوت مجموعه فازی و مجموعه کلاسیک

کلید درک مجموعه فازی مفهوم «درجه عضویت فازی» یا Membership degree است.

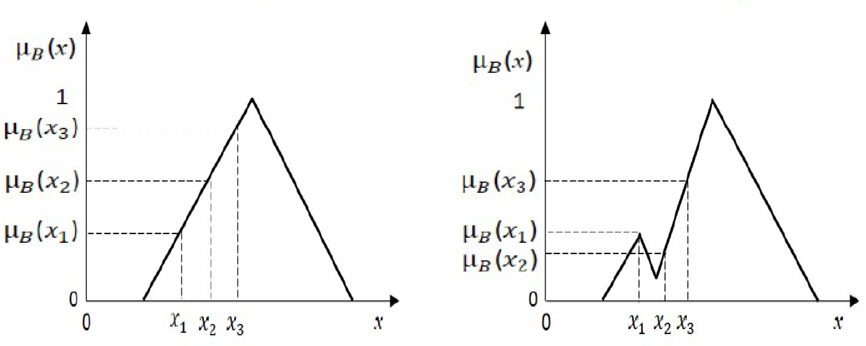
بیشتر برای نمایش مجموعه‌های فازی، از نموداری در مختصات دکارتی استفاده می‌کنند. محور افقی در این نمودار، مقدارهای مربوط به مجموعه U‌ و محور عمودی نیز درجه عضویت برای اعضای مجموعه را نشان می‌دهد. فرض کنید که می‌خواهیم مجموعه‌ای از طول قد افراد بالای ۱۸۰ و کمتر از آن بسازیم. نمودار زیر تفاوت بین این مجموعه در حالت فازی و عادی را نشان می‌دهد.

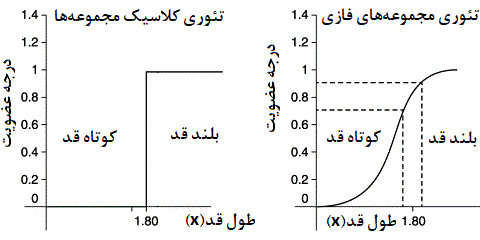
تفاوت مجموعه فازی و مجموعه کلاسیک

پشتیبان (تکیه گاه) مجموعه فازی

مجموعه پشتیبان Support set مجموعه فازی Ã، مجموعه‌ای قطعی شامل عناصری است که درجه عضویت آنها بزرگتر از صفر است. اگر مجموعه‌ای هیچ پشتیبانی نداشته باشد یک مجموعه فازی تهی خواهد بود.

Supp (Ã) = { x |x ∊ R‚ µÃ (x) > 0}

برش آلفا (α -cut)

برش آلفا یک مجموعه قطعی شامل عناصری است که درجه عضویتی حداقل برابر α داشته باشد. یک برش α بر یک مجموعه‌ فازی تعامل با آن را در سطح اطمینان α امکانپذیر می‌سازد.

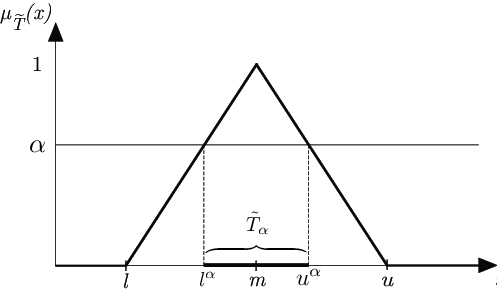
برش آلفا (عدد فازی مثلثی)

مثال ۱-۱- مجموعه دانشجویان درسخوان را به صورت زیر در نظر بگیرید:

a =18.5, b=14, c=19, d=20, e=16

à ={( α‚ ۰.۷۵)‚(b‚ ۰)‚(c‚ ۰.۸۵)‚(d‚ ۱)‚(e‚ ۰.۶۵)}

دو برش ۰.۶ و ۰.۷ روی مجموعه به صورت زیر اعمال می‌شود:

Ã_۰.۶ ={( α‚ ۰.۷۵)‚(c‚ ۰.۸۵)‚(d‚ ۱)‚(e‚ ۰.۶)}
Ã_۰.۷ ={( α‚ ۰.۷۵)‚(c‚ ۰.۸۵)‚(d‚ ۱)}

مجموعه فازی نرمال

یک مجموعه فازی زمانی نرمال است که در بین اعضای آن حداقل یک عضو با درجه عضویت یک وجود داشته باشد. به عبارت دیگر ارتفاع آن یک باشد. برای نرمال کردن یک مجموعه غیر نرمال می‌توان درجه عضویت تمام عناصر را بر بزرگترین درجه عضویت (ارتفاع) مجموعه تقسیم کرد.

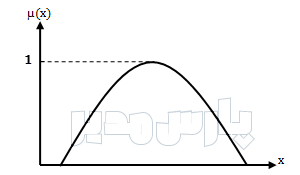
مجموعه فازی نرمال (حبیبی و آفریدی، ۱۴۰۱: ۵)

مجموعه فازی محدب

یک مجموعه فازی مانند Ã محدب است اگر:

μà (λx1+(1-λ)x2) ≥ min {μÃ(x1 ) , μÃ(x2)}

در رابطه بالا λ عددی بین صفر و یک است. مجموعه فازی Ã محدب است اگر تمامی برش‌های α آن محدب باشند.

مجموعه فازی محدب و غیرمحدب

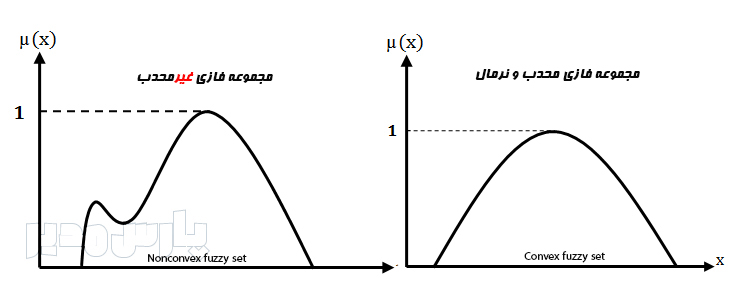
در نگاره بالا، هر دو مجـموعه نرمال هستند چون دست‌کم یک عضو با درجه عضویت یک دارند. همچنین مجـموعه سمت چپ، محدب است زیرا تمامی زوج‌های دلخواه آن، درونش قرار دارند. همچنین چون مجموعه پشتیبان محدودی دارد یک عدد فازی از نوع اعداد فازی مثلثی است. از سوی دیگر مجـموعه سمت راست، غیرمحدب است زیرا برخی زوج‌های آن مانند X2 درون آن قرار ندارند.

یک راه بسیار ساده برای تشخیص محدب بودن یک مجموعه این است که هر خط واصل بین دو نقطه دلخواه آن در مجموعه A قرار داشته باشد.

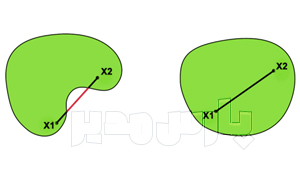
تشخیص محدب و غیرمحدب (حبیبی و آفریدی، ۱۴۰۱: ۶)

مجموعهٔ کوژ یا مجموعهٔ محدب، زیرمجموعه‌ای از فضای اقلیدسی است که هر ترکیب محدب از هر دو عضو دلخواه آن، عضوش باشد. به بیان دیگر، مجموعه‌ای را محدب می‌نامیم، که هر پاره‌خط واصل دو نقطهٔ دلخواه آن به طور کامل درونش قرار گیرد.

جمع بندی بحث

مجموعه، گردایه‌ای از اشیا است. هر یک از اشیا درون مجموعه را یک عضو (Element) می‌نامند. به این ترتیب مشخص است که یک مجموعه با اعضای آن تعیین می‌شود. در منطق فازی به جای استفاده از یک تابع نشانگر به عنوان تابع عضویت مجموعه A از یک تابع با شرایط ویژه، استفاده می‌شود. بنابراین به نظر می‌رسد برای مشخص کردن مجموعه فازی A باید از دو مولفه استفاده کرد به این معنی که ابتدا عضو و سپس درجه عضویت آن عضو را نام برد. به همین علت مجموعه‌های فازی مثل A را به صورت زوج مرتب Ã=(X, μ) نشان می‌دهند که مولفه اول اعضا و مولفه دوم نیز درجه عضویت را نشان می‌دهد.

منبع: حبیبی، آرش؛ آفریدی، صنم. (۱۴۰۱). تصمیم‌گیری چندشاخصه، تهران: انتشارات نارون.