منطق فازی و کاربرد آن در مدیریت

منطق فازی (Fuzzy Logic) بازنگری در شیوه استدلال علمی مبتنی بر الگوی واقعی اندیشه انسانی میباشد. این شیوه اندیشه، نخستین بار با عنوان نظریه ابهام یا vagueness توسط مکس بلک مطرح شد. لطف علی عسگرزاده در سال ۱۹۶۵ براساس مطالعات مکس بلک منطق فازی یا را مطرح کرد. منطق فازی در مقابل منطق دودویی ارسطویی قرار میگیرد. منطق فازی که در فرهنگ لغت شرایط عدم قطعیت و نامعلوم تعریف شده است، معتقد است ابهام در ماهیت علم است.
لطفی زاده اینطور استدلال کرد که بشر به ورودیهای اطلاعاتی دقیق نیازی ندارد بلکه قادر است تا کنترل تطبیقی میان اطلاعات موجود انجام دهد. بنابراین، این منطق در ابتدا بهعنوان روشی برای پردازش اطلاعات معرفی شد و برخلاف منطق ارسطویی به جای پرداختن به صفر و یک، از صفر تا یک را مورد بررسی و تحلیل قرار میدهد و بر مفهوم درستی نسبی، دلالت میکند. بدین صورت به اعمال و طرز فکر آدمیان بیشتر نزدیک میشود.
لطفی زاده نام فازی Fuzzy را روی این مجموعههای گنگ یا منطق چند ارزشی قرار داد. مجموعه هایی که اجزایشان با درجات مختلف به آنها تعلق دارند. نظیر افرادی که میزان رضایت خود را از مجموعه کار با درجات مختلف خیلی راضی، راضی، بی تفاوت و … بیان میکنند. حال با این توصیفات اگر از ما پرسیده شود منطق فازی چیست شاید ساده ترین پاسخ بر اساس شنیدهها این باشد که یک نوع منطق است که روشهای نتیجهگیری در مغز بشر را جایگزین میکند. کاربرد منطق فازی گسترده است بنابراین در ادامه بر کاربرد منطق فازی در مدیریت تاکید میشود.
تعریف منطق فازی
برای تعریف و شناخت منطق فازی هیچ واژه و عبارت پیچیدهای نیاز نیست. زمانی که انسان اندیشه را آغاز کرد و برای بیان اندیشه خود از زبان استفاده کرد، منطق فازی شکل گرفت. انسان نخستین میتوانست بگوید هوا گرم، سرد و یا اینکه معتدل است. نیازی به هیچ آداب و ترتیب خاصی هم نبود. اما وقتی منطق علمی مبتنی بر تفکر ارسطویی شکل گرفت نوع جدیدی از شیوه اندیشه پیرامون پدیدهها جایگزین دیدگاه انسان آزاد شد. در این شیوه علمی همه پدیدها حالت دو وجهی پیدا کردند و اندیشیدن تابع یک نظم علمی گردید. منطق فازی در واقع راهی برای شکستن همین نظم علمی منطبق بر تفکر دو ارزشی است. به دیگر سخن منطق فازی راهی برای اندیشیدن علمی به شیوه انسان پیش از دوران منطق علمی است.
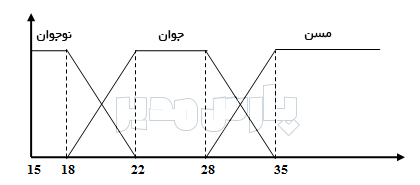
فازیسازی متغیر سن
منطق فازی نیز یک منطق چند ارزشی است که طیفی خاکستری را در دو کران سیاه و سپید در برمیگیرد. ماکس بلک (۱۹۰۹- ۱۹۸۹، باکو) به سال ۱۹۳۷ مقالهای با نام «ابهام » را در مجله «فلسفه علم» منتشر کرد. بلک برای اولین بار مفاهیمی که اکنون با عنوان منحنی عضویت شناخته میشود را مطرح کرد. نظریه بلک مورد اقبال قرار نگرفت و راهی در جهان علم باز نکرد. اما پس از بلک، لطفی زاده با تغییر نام «ابهام» به «فازی » راهی تازه برای پذیرش این ایده باز کرد. لطفی زاده در سال ۱۹۶۵ مقالهای تحت عنوان «مجموعههای فازی» در مجله «اطلاعات و کنترل» منتشر ساخت. در واقع او آن چیزی را که منتقدان منطق ارسطویی با نام «ابهام» یا «چند ارزشی» مطرح کرده بودند، «فازی» نامید.
مجموعه فازی
درک مفهوم «مجموعه فازی» در کانون یادگیری منطق فازی قرار دارد. به دیگر سخن منطق فازی را میتوان استدلال با مجموعههای فازی بیان کرد. مجموعههای فازی در قیاس با مجموعههای کلاسیک و مفهوم درجه عضویت قابل تشریح است. در یک مجموعه کلاسیک هر یک از اجزا مجموعه دارای درجه عضویت یک بوده و سایر عناصر درجه عضویت صفر دارند. یعنی یک عنصر یا عضوی از مجموعه A است و یا عضو آن نیست. مجموعههای فازی برخلاف مجموعههای کلاسیک، دارای مرزهای مشخص و خوب تعریف شدهای نیست.
برای نمونه براساس مکتب کلاسیک، دانش آموزی که نمره ۹٫۵ میگیرد در مجموعه مردود قرار گرفته و دانشآموزی که نمره ۱۰٫۵ میگیرد در مجموعه قبول قرار میگیرد. اکنون این پرسش مطرح میشود: آیا تفاوت این دو نفر در آن حد است که نفر اول باید یکسان از نفر دوم عقب بماند. اینگونه تعریف از یک ارزش آستانه مطلق برای شمول افراد در یک مجموعه در منطق کلاسیک جای دارد. منطق فازی مفاهیم ضروری جدیدی را در قالب عدم اطمینان و ابهام وارد ریاضیات و منطق کرده و مبانی علم کلاسیک را متحول ساخته است. کلید درک مجموعه فازی مفهوم «درجه عضویت» است.
درجه عضویت
درجه عضویت دیگر مفهوم کانونی منطق فازی است. لطفی زاده در مقاله خود برای تشریح مفهوم منطق فازی از مثال قد انسان استفاده کرد، در این مثال وی از مفهوم «منحنی عضویت » استفاده کرد. این منحنی برای اندازه از قد، درجه عضویتی را مشخص میکند. منحنی عضویت لطفی زاده درست مانند منحنی ارائه شده توسط بلک عمل میکند.
در منطق کلاسیک تعلق یا عضویت یک عضو به یک مجموعه مفهومی کاملاً قطعی و دقیق است. بنابراین یک شی یا عضو یک مجموعه است و یا نیست. پس تابع عضویت فقط میتواند دو مقدار ۰ و ۱ را داشته باشد. به منظور توصیف تغییرات تدریجی و اندک لطفی زاده درجات بین ۰ و ۱ و مفهوم درجه عضویت یا تابع عضویت را معرفی کرده است. برای این منظور تابع عضویت µ تعریف میشود که همواره مقادیری از بازه [۰و۱] را شامل میشود. یک عدد فازی به وسیله یک بازه از اعداد حقیقی که هر کدام یک درجه عضویت بین ۰ و ۱ را دارند مشخص میشود.
اعداد فازی
اعداد فازی نوعی خاص از مجموعههای فازی هستند. بنابراین با درک مفهوم مجموعه فازی میتوان اعداد فازی را بسادگی فرا گرفت. در منطق کلاسیک هر عدد یک مقدار قطعی و مشخص است اما در منطق فازی هر عدد مقداری تقریبی است. عدد فازی یک مجموعه فازی با شرایط سهگانه زیر است:
- نرمال باشد
- محدب باشد
- مجموعه پشتیبان آن محدود باشد.
انواع بسیار متنوعی از اعداد فازی با نامها و ویژگیهای متفاوت ارائه شده و بکار گرفته شده است. اما یک اصل مهم در بکارگیری تئوری فازی کارایی محاسباتی آن است. کار کردن با اعداد فازی مختلف دشواریهای زیادی دارد. دیدیه دوبوا و هنری پراد برای رفع این مشکل اعداد فازی «راست و چپ» موسوم به اعداد LR را معرفی کردند. اما این روش نیز پیچدگیهای زیادی دارد و کمتر مورد استفاده قرار گرفته است. در این میان بیشترین کاربرد را اعداد فازی مثلثی و ذوزنقهای دارند. این اعداد در علوم اجتماعی و مدیریت بسیار مورد استفاده قرار میگیرد. تمرکز این کتاب بر اعداد فازی مثلثی است. البته به فازی ذوزنقهای نیز اشاره خواهد شد.
جمعبندی بحث منطق فازی
کاربرد مجموعههای فازی در تصمیمگیری یکی از مهمترین کاربردهای این تئوری در مقایسه با تئوریهای کلاسیک میباشد. در واقع تئوری تصمیمگیری فازی تلاش میکند که ابهام و عدم قطعیتهای ذاتی موجود در ترجیحات، اهداف و محدودیتهای موجود در مسائل تصمیمگیری را در مدل احراز کند. همواره در مدلهای تصمیمگیری بهتر است که تصمیم بستگی کمتری به سیستم دو جوابی بلی و خیر داشته باشد زیرا اگر جواب نادرست باشد خطا ۱۰۰% خواهد بود و این خطا اثر زیادی روی مدل تصمیمگیری خواهد داشت.
با استفاده از مجموعههای فازی خطا کاهش پیدا میکند. در رویکردهای تصمیمگیری چندمعیاره، اگر چه از شایستگیها و تواناییهای ذهنی خبرگان برای انجام مقایسات استفاده میشود، اما کمی کردن دیدگاه خبرگان به روش سنتی، امکان انعکاس کامل سبک تفکر انسانی را ندارد. استفاده از مجموعههای فازی، سازگاری بیشتری با توضیحات زبانی و بعضاً مبهم انسانی دارد و بنابراین بهتر است که با بکارگیری اعداد فازی به تصمیمگیری در دنیای واقعی پرداخت.
فهرست مطالب کتاب تصمیمگیری چندشاخصه فازی
منبع: حبیبی، آرش؛ آفریدی، صنم. (۱۴۰۱). تصمیمگیری چندشاخصه، تهران: انتشارات نارون.
تصمیم گیری چندمعیاره | ۰۷ بهمن ۹۵