برازش حداقل مربعات جزئی

برازش حداقل مربعات جزئی (Model Fit) نشان می‌دهد تا چه میزان مدل نظری ارائه شده با مدل تجربی که توسط پژوهشگر اجرا شده، هماهنگی دارد. تعداد این شاخص‌ها در حداقل مربعات جزئی نسبت به مدل معادلات ساختاری محدودتر است.

به‌طور کلی از شاخص‌های برازش مدل برای سنجش شباهت میان منحنی‌های تجربی و منحنی‌های نظری استفاده می‌شود. در مدل معادلات ساختاری از شاخص‌های برازش مدل برای ارزیابی بخش ساختاری استفاده می‌شود. با توسعه نرم‌افزارهای حداقل مربعات جزئی امکان محاسبه برخی از شاخص‌های برازش در این نرم‌افزار نیز وجود دارد. در این آموزش کوشش بر آن است تا پژوهشگران با انواع شاخص‌های برازندگی مدل در حداقل مربعات جزئی آشنا شوند.

شاخص‌های برازش حداقل مربعات جزئی

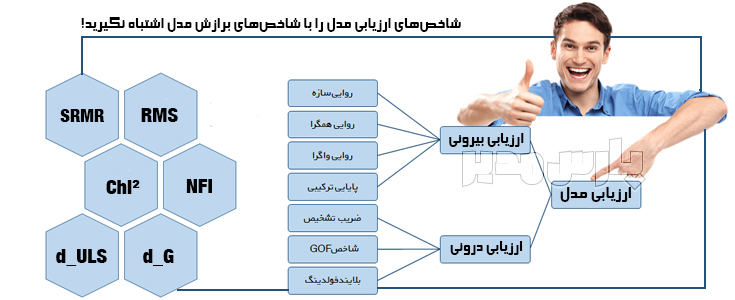
شاخص‌های برازش حداقل مربعات جزئی در نرم‌افزار Smart PLS 3 به استناد سایت سازنده این نرم‌افزار (مشاهده منبع) عبارتند از:

• شاخص ریشه میانگین مربعات باقیمانده استاندارد (SRMR)
• معیار تناسب مدل راستین d_ULS و d_G
• شاخص تناسب به‌هنجار (NFI)
• خی دو (Chi²)
• شاخص تتای ریشه میانگین مربعات (RMS_theta)

مشاهده شاخص‌های برازش حداقل مربعات جزئی

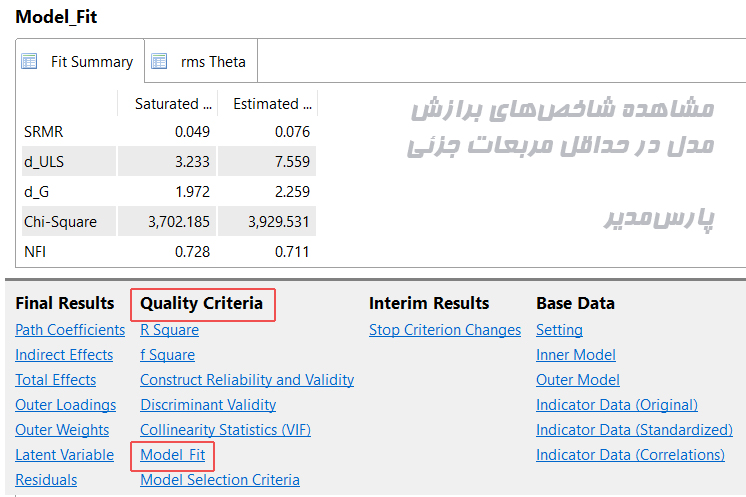
برای محاسبه این شاخص‌ها باید مدل را در حالت الگوریتم حداقل مربعات جزئی (PLS Algorithm) اجرا کنید. در نتایج حاصل از قسمت معیارهای کیفیت (Quality Criteria) روی گزینه تناسب مدل (Model Fit) کلیک کنید. شاخص‌های برازش قابل مشاهده خواهد بود.

شاخص ریشه میانگین مربعات باقیمانده استاندارد (SRMR)

شاخص SRMR به عنوان تفاوت بین همبستگی مشاهده شده و ماتریس همبستگی ضمنی مدل تعریف می‌شود. این شاخص امکان ارزیابی میانگین بزرگی اختلافات بین همبستگی های مشاهده شده و مورد انتظار را به عنوان معیار مطلق معیار برازش (مدل) فراهم می کند.

اگر مقدار شاخص SRMR از ۰/۱ کمتر باشد نشان از برازش مطلوب است. برخی نیز مقدار سخت‌گیرانه ۰/۸ را پیشنهاد کرده‌اند به این معنا که شاخص ریشه میانگین مربعات باید کمتر از ۰/۰۸ باشد. هنسلر و همکاران (۲۰۱۴) شاخص SRMR را به عنوان یک معیار مناسب برای PLS-SEM معرفی کردند که می تواند برای جلوگیری از تعیین نادرست مدل استفاده شود.

معیارهای تناسب مدل راستین

دو معیار فاصله اقلیدسی (d_ULS) و فاصله ژئودزیکی (d_G) برای ارزیابی برازش مدل در حداقل مربعات جزئی با عنوان معیارهای تناسب راستین شناخته می‌شوند. این دو معیار و کاربردهای آن در مدل‌های ساختاری بسیار ناشناخته است. تاکنون مطالعات بسیاری کمی در این زمینه انجام شده است و دانش پژوهشگران پیرامون آنها اندک است. کاندوس و دبرا از این معیارها برای محاسبه اختلاف از ماتریس‌های کوواریانس استفاده کرده‌اند.

به‌طور مشخص این دو معیار عدد دقیقی به عنوان شاخص به‌دست نمی‌دهند. به دیگر سخن هیچ شدت آستانه‌ای وجود ندارد که بتوان براساس آن اظهار نظر کرد. برای نمونه اگر مقدار NFI بالای ۰/۷ باشد برازش مدل مناسب است اما برای معیارهای تناسب مدل راستین چنین آستانه‌ای وجود ندارد. پژوهشگران بارها از من پرسیده‌اند در این صورت چه باید کرد؟ شما باید مقدار بوت‌استراپینگ را برای این مقادیر با روش بولن-اشتاین (Bollen-Stine) محاسبه کنید. برای این منظور از گزینه complete در bootstrapping استفاده کنید. اگر این مقادیر کوچکتر از کران بالای فاصله اطمینان بوت استراپینگ باشند، برازش مناسب است.

شاخص تتای ریشه میانگین مربعات (RMS_theta)

شاخص RMS_theta ریشه میانگین مربعات ماتریس کوواریانس باقیمانده مدل خارجی است (لوهمولر، ۱۹۸۹). این معیار برازش تنها برای ارزیابی مدل‌های انعکاسی مفید است، زیرا باقی‌مانده‌های مدل بیرونی برای مدل‌های اندازه‌گیری تکوینی معنی‌دار نیستند.

تتای RMS درجه همبستگی باقیمانده های مدل بیرونی را ارزیابی می‌کند. اندازه‌گیری باید نزدیک به صفر باشد تا برازش مدل خوب را نشان دهد زیرا به این معنی است که همبستگی بین باقیمانده‌های مدل بیرونی بسیار کوچک است (نزدیک به صفر).

تتای RMS بر روی باقیمانده‌های مدل بیرونی ایجاد می شود، که تفاوت بین مقادیر شاخص پیش بینی شده و مقادیر شاخص مشاهده شده است. برای پیش بینی مقادیر اندیکاتور لازم است در PLS-SEM امتیاز متغیرهای نهفته وجود داشته باشد. مقادیر RMS_theta زیر ۰.۱۲ نشان‌دهنده یک مدل مناسب است، در حالی که مقادیر بالاتر نشان دهنده عدم تناسب است (Henseler et al., 2014).

شاخص نیکویی برازش (GOF)

شاخص نیکویی برازش (GOF) یا Goodness of Fit  برازش بخش ساختاری و اندازه‌گیری را به صورت همزمان بررسی می‌کند. از آنجایی که GoF نمی‌تواند به طور قابل اعتماد مدل‌های معتبر را از نامعتبر تشخیص دهد و از آنجایی که کاربرد آن به تنظیمات مدل خاصی محدود می شود، پژوهشگران باید از استفاده از آن به عنوان معیار مناسب خودداری کنند. GoF ممکن است برای تحلیل چندگروهی (PLS-MGA) مفید باشد (مشاهده منبع).

این شاخص با استفاده از میانگین هندسی شاخص R^۲ و میانگین شاخص‌های اشتراکی قابل محاسبه است. معیار GOF توسط تننهاوس و همکاران (۲۰۰۴) ابداع گردید و طبق رابطه زیر محاسبه می‌شود.

GOF = √average (Commonality) × average (R^۲)

از آنجا که در حداقل مربعات جزئی مقدار Commonality با AVE برابر است وتزلس و همکاران (۲۰۰۹) فرمول زیر را ارائه کرده‌اند:

GOF = √average (AVE) × average (R^۲)

وتزلس و همکاران (۲۰۰۹) سه مقدار برای ارزیابی شاخص GOF در نظر گرفته‌اند:

• ضعیف: اگر بین ۰/۱ تا ۰/۲۵ باشد.
• متوسط اگر بین ۰/۲۵ تا ۰/۳۶ باشد.
• قوی: اگر از ۰/۳۶ بیشتر باشد.

تننهاوس و همکاران معتقدند شاخص GOF در مدل PLS راه حلی عملی برای این مشکل بررسی برازش کلی مدل است. این شاخص همانند شاخص‌های برازش در روش‌های مبتنی بر کوواریانس عمل می‌کند. همچنین می‌توان از آن برای بررسی اعتبار یا کیفیت مدل PLS به صورت کلی استفاده کرد. این شاخص نیز همانند شاخص‌های برازش مدل لیزرل عمل می‌کند و بین صفر تا یک قرار دارد و مقادیر نزدیک به یک نشانگر کیفیت مناسب مدل هستند. البته هنسلر استفاده از این شاخص را زیر سوال برده است و اعتقاد چندانی به آن ندارد.

ارزیابی بخش ساختاری مدل

در روش حداقل مربعات جزئی شاخص‌هایی برای ارزیابی بخش ساختاری مدل وجود دارد. بسیاری پژوهشگران به اشتباه این شاخص‌ها را به عنوان شاخص‌های برازش مدل در نظر می‌گیرند. مهم‌ترین شاخص‌های ارزیابی بخش ساختاری (درونی) مدل در روش حداقل مربعات جزئی شامل اندازه اثر F^۲ ، ضریب تعیین R^۲، شاخص Q^۲ است.

ضریب تعیین R^۲

ضریب تعیین R^۲ معیاری است که بیانگر میزان تغییرات هر یک از متغیرهای وابسته مدل است که به وسیله متغیرهای مستقل تبیین می‌شود. مقدار R^۲ تنها برای متغیرهای درون‌زای مدل ارائه می‌شود و در مورد سازه‌های برون‌زا مقدار آن برابر صفر است. هرچه مقدار R^۲ مربوط به سازه‌های درون‌زای مدل بیشتر باشد، نشان از برازش بهتر مدل است.

سه مقدار ۰/۱۹، ۰/۳۳ و ۰/۶۷ به عنوان مقادیر ضعیف، متوسط و قوی برای ضریب تعیین معرفی شده است (چین، ۱۹۹۸ : ۳۲۳). البته باید دقت کنید چین این مقادیر را در زمینه یک مدل بخصوص ارائه کرده است اما در مطالعات پژوهشگران ایرانی به عنوان یک اصل ثابت مورد استفاده قرار می‌گیرد.

شاخص ارتباط پیش‌بین Q^۲

دومین شاخص قدرت پیش‌بینی مدل، شاخص ارتباط پیش‌بین یا Q^۲ است. این معیار که توسط استون و گیسر (۱۹۷۵) معرفی شد، قدرت پیش‌بینی مدل در سازه‌های درون‌زا را مشخص می‌کند. به اعتقاد آنها مدل‌هایی که دارای برازش ساختاری قابل قبول هستند، باید قابلیت پیش‌بینی متغیرهای درون‌زای مدل را داشته باشند. بدین معنی که اگر در یک مدل، روابط بین سازه‌ها به درستی تعریف شده باشند، سازه‌ها تاثیر کافی بر یکدیگر گذاشته و از این راه فرضیه‌ها به درستی تائید شوند.

اگر مقدار شاخص Q^۲ مثبت باشد نشان می‌دهد که برازش مدل مطلوب است و مدل از قدرت پیش‌بینی کنندگی مناسبی برخوردار است (هنسلر و همکاران، ۲۰۰۹ : ۳۰۳).

یرای محاسبه شاخص Q^۲ از تکنیک بلایندفولدینگ استفاده می‌شود. همانطور که در ویدیوی آموزشی بلایندفولدینگ ارائه شده است این تکنیک دو مقدار را ارائه می‌کند که به صورت CV-Com و CV-Red در شکل نمایش داده می‌شود. از مقدار روایی متقاطع افزونگی (CV-Red) به عنوان برآورد شاخص استون-گیزر استفاده می‌شود (چین، ۱۹۹۸ : ۳۱۸).

شاخص اندازه اثر F^۲

اندازه اثر دیگر شاخص ارزیابی بخش ساختاری مدل است و برای متغیرهای مستقل برونزا مصداق دارد. شاخص اندازه اثر توسط جاکوب کوهن معرفی شده است و در بحث محاسبه شاخص کوهن نیز به آن پرداخته شده است. شاخص F^۲ برای یک متغیر مستقل، میزان تغییرات در برآورد متغیر وابسته را زمانی که اثر آن متغیر حذف شود را نشان می‌دهد.

براساس نظر کوهن (۱۹۸۸) میزان این شاخص به ترتیب ۰/۰۲ (ضعیف) ۰/۱۵ (متوسط) و ۰/۳۵ (قوی) می‌باشد.

• کمتر از ۰/۰۲ : قدرت پیش‌بینی اندک
• بین ۰/۰۲ تا ۰/۱۵ : قدرت پیش‌بینی متوسط
• بین ۱۵/۰ تا ۰/۳۵ : قدرت پیش‌بینی خوب

برای محاسبه اندازه اثر از میزان ضریب تعیین استفاده می‌شود.

f^۲=(R^۲_{included –} R^۲_excluded) / (۱ – R^۲_included)

براساس رابطه فوق کافی است یک بار ضریب تعیین با در نظر گرفتن تاثیر متغیر مستقل موردنظر محاسبه شود و سپس با حذف این تاثیر محاسبه شود. سپس مقدار محاسبه شده براساس مقادیر پیشنهادی کوهن تفسیر شود.

فهرست منابع

حبیبی، آرش؛ جلال‌نیا، راحله. (۱۴۰۱). کتاب حداقل مربعات جزئی. تهران: انتشارات نارون.

Chin, W. W. (1998). The partial least squares approach to structural equation modeling. Modern methods for business research, 295(2), 295-33.

Hair, J. F., Hult, G. T. M., Ringle, C. M., and Sarstedt, M. (2017). A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM), 2nd Ed., Sage: Thousand Oaks.

Henseler, J., Ringle, C. M., & Sinkovics, R. R. (2009). The use of partial least squares path modeling in international marketing. In New challenges to international marketing. Emerald Group Publishing Limited.

Henseler, J., Dijkstra, T. K., Sarstedt, M., Ringle, C. M., Diamantopoulos, A., Straub, D. W., … & Calantone, R. J. (2014). Common beliefs and reality about partial least squares. Organizational Research Methods, 17(2), 182-209.

Lohmöller, J.-B. (1989). Latent Variable Path Modeling with Partial Least Squares, Physica: Heidelberg.

Wetzels, M., Odekerken-Schröder, G., & Van Oppen, C. (2009). Using PLS path modeling for assessing hierarchical construct models: Guidelines and empirical illustration. MIS quarterly, 177-195.

https://www.smartpls.com/documentation/algorithms-and-techniques/model-fit/