آزمون کروسکال-والیس

آزمون کروسکال-والیس (Kruskal-Wallis) یک آزمون آمار ناپارامتریک است و برای بررسی اختلاف میانگین چند جامعه آماری استفاده می‌شود. از این روش برای آزمون پیروی نمونه‌ها از یک توزیع نیز استفاده می‌شود. این آزمون با عنوان آزمون H نیز شناخته می‌شود و به نام دو دانشمند ویلیام کروسکال و آلن والیس نامگذاری شده است. این روش برای بررسی کردن دو یا چند گروه نمونه با تعداد نمونه‌های یکسان یا متفاوت به‌کار می‌رود. این آزمون حالت تعمیم‌یافته‌ی آزمون یو مان-ویتنی است که فقط توانایی مقایسه‌ی دو گروه نمونه را دارد. آزمون کروسکال-والیس معادل روش پارامتریک آنالیز واریانس تک عاملی است.

همان‌طور که می‌دانیم این آزمون غیر پارامتری است. بنابراین بر عکس تحلیل واریانس یک‌راهه این آزمون فرضی روی نرمال بودن توزیع ارور ندارد. اگر این فرض را بکنیم که نمودار تمام گروه‌ها صرف نظر از میانگینشان یک شکل و مقیاس هستند در این صورت فرض صفر ما برابر بودن میانگین گروه‌هاست و فرضیه مقابل نیز نابرابر بودن این میانگین‌ها در حداقل یک گروه است. زمانی که فرض‌های بنیادی تحلیل واریانس مانند نرمال بودن توزیع داده‌ها و برابری واریانس گروه‌ها برقرار نباشد، از آزمون کروسکال والیس استفاده می‌شود. به همین دلیل گاهی به این آزمون «تحلیل واریانس رتبه ای» نیز گفته می‌شود. این آزمون می‌تواند در مورد داده‌های پیوسته (فاصله‌ای یا نسبی) نیز به کار برده شود، در این حالت باید توجه شود که داده‌ها به صورت داد‌های رتبه‌ای تبدیل شده و مورد استفاده قرار می‌گیرد.

انجام آزمون کروسکال-والیس در SPSS

در آزمون رضایت کاربران سایت پارس مدیر اگر بخواهیم تفاوت رضایت دانشجویان ۴ گرایش مختلف (مدیریت بازاریابی، مدیریت مالی، مدیریت صنعتی و مهندسی صنایع) را بسنجیم باید از تکنیک تحلیل واریانس استفاده کنیم. اگر فرض نرمال بودن برقرار نباشد از معادل ناپارامتریک آن یعنی آزمون کروسکال-والیس استفاده می‌شود. آزمون فرض آماری به صورت زیر است:

H0 : µ­­۱ = µ­­۲ = µ­­۳ = µ­­۴

H1 : µ­­i ≠ µ­­j

نرم‌افزار SPSS را باز کنید.

در زبانه Variable View پس از تعریف متغیر Student ارزش‌هایی مانند زیر را تعیین کنید:

۱ = Marketing; 2 = Finance; 3 = MIndustrial; 4 = EIndustrial

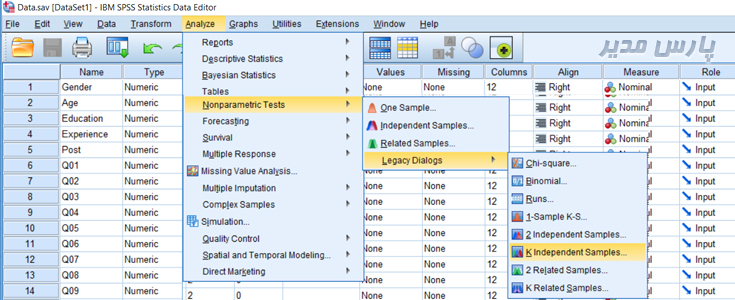
برای استفاده از آزمون کروسکال-والیس فرمان زیر را اجرا کنید:

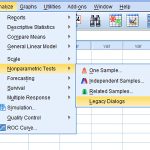
Analyze→ Nonparametric Tests → k independent Samples

در کادر ظاهر شده گزینه kruskal-wallis را فعال کنید.

متغیر رضایت (Satisfaction) را به کادر Test variable list منتقل کنید.

متغیر چند مقوله‌ای در اینجا رشته تحصیلی (Student) را به کادر Grouping Variable منتقل کنید.

روی تگمه Define variable کلیک کنید.

در کادر ظاهر شده  اعداد ۱ و ۴ را وارد کرده و سپس دکمه Continue را بزنید. دقت کنید چون برای اولین رشته عدد ۱ و برای آخرین رشته عدد ۴ در ظنر گرفته شده است و دراینجا می‌خواهیم براساس هر چهار رشته مقایسه صورت گیرد این اعداد وارد شده است. در کادر اصلی نیز دکمه OK را بزنید.

برونداد آزمون در یک صفحه مجزا باز می‌شود. نتیجه حاصل چند قسمت دارد. در جدول اول نتایج آمار توصیفی مانند میانگین و انحراف معیار آمده است.

فرض کنید مقدار معناداری رابطه رشته تحصیلی با متغیر رضایت ۰/۰۲۶ بدست آمده است. بنابراین در سطح خطای ۵% فرض صفر رد می‌شود. یعنی رشته تحصیلی با میزان رضایت از سایت رابطه دارد.

آزمون تعقیبی کروسکال-والیس

آزمون بونفرینی یا آزمون دان (Dunn) یک روش ناپارامتریک است که از همان رتبه‌بندی مشترکی که توسط کروسکال-والیس محاسبه شده است استفاده می‌کند. همچنین از همان واریانس تلفیقی استفاده می‌کند که با فرضیه صفر آزمون کروسکال-والیس بیان می‌شود. آزمون دان از همان داده‌های Kruskal-Wallis برای آزمایش اختلاف بین هر دو گروه استفاده می‌کند.

به طور مشخص، تقریب آزمون z دان (۱۹۶۴) به عنوان تفاوت در میانگین نمرات رتبه تقسیم بر برآورد واریانس ادغام رتبه برای دو گروه محاسبه می‌شود. این آزمون از مسیر آزمون ANOVA قابل دسترسی است اما زیرمجموعه آزمون ANOVA نیست بنابراین می‌توانید از نتایج آن برای تفسیر تفاوت گروه‌ها در آزمون کروسکال و والیس بهره بگیرید.

مسیر دسترسی به این آزمون در آموزش آزمون‌های تعقیبی ارائه شده است.

نتیجه‌گیری

آزمون کروسکال-والیس یکی از روش‌های آمار ناپارامتریک در آمار استنباطی است که در دسته آزمون‌های میانگین جامعه قرار می‌گیرد. برای انجام دستی محاسبات با استفاده از این روش تمام داده‌ها را بدون در نظر گرفتن گروه‌ها از جایگاه ۱ تا N مرتب می‌شوند. به مقادیر مساوی نیز میانگین جایگاهی که در صورت برابر نبودن می‌گرفتند داده می‌شود. این آزمون به سادگی با استفاده از نرم‌افزار SPSS قابل انجام است. در خروجی محاسبات انجام شده در این روش، ملاک اصلی اظهارنظر مقدار معناداری است. چنانچه مقدار معناداری از سطح خطا کوچکتر باشد در این صورت میانگین مشاهده شده برای گروه‌ها تفاوت معناداری باهم دارد. در غیر اینصورت اختلاف میانگین مشاهده شده معنادار نیست.

منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: نارون.