توان آزمون

توان آزمون (Power of a test) به میزان احتمال رد فرض صفر زمانیکه فرض صفر واقعا اشتباه باشد، اشاره دارد. به زبان آماری به میزان احتمال رد فرض پوچ (H0) زمانیکه فرض بدیل (H1) درست باشد در آمار، توان آزمون گفته می‌شود.

در آزمون فرض آماری، توان آزمون می‌تواند بین ۰ تا ۱ باشد و هرچه بیشتر در نظر گرفته شود احتمال خطای نوع دوم بیشتر می‌شود. توان آزمون با دو مفهوم «خطای نوع اول» و «خطای نوع دوم» همراه است.

خطای نوع یک: رد فرض صفر زمانیکه فرض صفر درست است.

خطای نوع دو: رد نکردن فرض صفر زمانیکه فرض صفر نادرست است.

توان آماری یک آزمون، احتمال آن است که پژوهشگر فرضیه صفر را رد کند وقتی فرضیه در واقع نادرست است. چون بیشتر آزمون‌های آماری در شرایطی انجام می‌شوند که عامل اصلی (treatment)، حداقل کمی اثر روی نتیجه دارد، توان آماری به صورت احتمال اینکه آن آزمون “منجر به نتیجه‌گیری درستی در مورد فرضیه صفر می‌شود”، تعبیر می‌شود.

خطای نوع یک و خطای نوع دو

فاصله اطمینان و خطای نوع ۱

فاصله اطمینان (Confidence interval) میانگین تخمین بعلاوه منهای واریانس تخمین است. به عبارت دیگر فاصله اطمینان دامنه‌ای از مقادیر موردانتظار در صورت تکرار آزمون را نشان می‌دهد. هر آزمون با میزانی از خطا همراه است که با α نشان داده می‌شود. همیشه ادعای آزمون در فرض بدیل (H1) و خلاف ادعا در فرض پوچ (H0) مطرح می‌شود. هدف از آزمون آماری رد فرض صفر است تا ادعا ثابت شود اگر فرض صفر رد شود درحالیکه در واقع صحیح باشد، خطای نوع ۱ رخ می‌دهد. احتمال اینکه فرض صفر زمانی که واقعاً درست باشد، تائید شود با فاصله اطمینان (۱-α) نشان داده می‌شود.

در هر آزمون ابتدا باید سطح اطمینان را مشخص کرد. به‌طور معمول سطح اطمینان ۹۵% و گاهی نیز ۹۹% درنظر گرفته می‌شود.

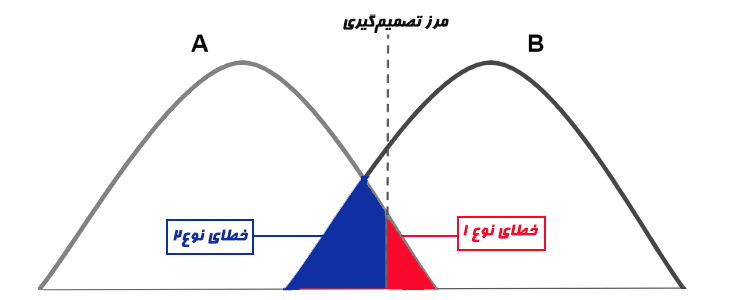
سطح اطمینان یک مرز تصمیم‌گیری ایجاد می‌کند. مقادیری که بالاتر از این محدوده باشند بخشی از توزیع B در نظر گرفته می‌شوند و از فرض بدیل (ادعای آزمون) حمایت می‌کنند. مقادیری هم که پایین‌تر از این محدوده باشند، جزء توزیع A به شمار رفته و از فرض اولیه (پوچ) حمایت می‌کنند.

توان آزمون و خطای نوع ۲

در شکل سرآیند آموزش، ناحیه قرمز مقادیری است که در صورت جایگذاری اشتباه در توزیع B، همچنان قابل قبول خواهند بود. تعیین این مرز تصمیم‌گیری و آمادگی برای پاسخ‌های اشتباه، الزامی است. زیرا بین این دو توزیع مقداری همپوشانی وجود دارد که می‌تواند ابهام‌آور باشد. قسمت سایه‌خورده مقادیری از برچسب حقیقی داده ها  هستند که از فرض اولیه پشتیبانی می‌کنند (توزیع A)، اما ما آن‌ها را به اشتباه در حمایت از فرض مخالف (توزیع B) در نظر می‌گیریم. به همین دلیل آن‌ها را مثبت کاذب می‌نامیم؛ چون به اشتباه از پاسخ مثبت پشتیبانی می‌کنند. برای واضح‌تر کردن مبحث یک مثال می‌زنیم. فرض کنید سطح اطمینان ۹۵% و آلفا ۵% است. ناحیه‌ قرمز شکل ۵% از ناحیه‌ی زیر منحنی A را به خود اختصاص می‌دهد.

توان یک تست برابر است با احتمال این که به درستی از ادعای آزمون پشتیبانی شود و در شکل در قسمت B قرار دارد. توان آزمون به صورت β-۱ محاسبه می‌شود. بتا احتمال پذیرش فرض اولیه است حتی اگر فرض مخالف درست باشد. یعنی احتمال این‌که یک مقدار را به اشتباه جزئی از توزیع A در نظر بگیریم، در حالی‌که واقعاً متعلق به توزیع B است. معیار استاندارد توان آزمون اغلب ۰/۸ یا ۸۰% است، در نتیجه بتا هم معمولاً ۰/۲ یا ۲۰% در نظر گرفته می‌شود. علاوه بر موارد قبلی، سطح بتا را نیز باید متناسب با آزمایش خود تعیین کنید.

در شکل سرآیند این آموزش ناحیه آبی نشان‌دهنده‌ی بتا است. همانطور که در تصویر می‌بینید، این مقادیر در توزیع A قرار گرفته‌اند (در پشتیبانی از فرض اولیه) در حالی‌که باید بخشی از توزیع B باشند و بدین ترتیب اثری منفی روی نتیجه‌ی آزمایش می‌گذارند. به همین دلیل، داده‌های این ناحیه را منفی کاذب می‌خوانیم. این خطای آزمایشی را به نام خطای نوع II (خطای نوع دو) نیز می‌شناسند.

کاربرد توان آزمون در نمونه‌گیری

یکی از کاربردهای توان آزمون در محاسبه حجم نمونه برای مدل معادلات ساختاری و حداقل مربعات جزئی است. هر چه میزان توان آزمون بیشتر شود حجم نمونه بیشتری مورد نیاز خواهد بود.

سطح توان موردانتظار (Desired statistical power level) به صورت عرف ۰/۸ در نظر گرفته می‌شود اما پژوهشگران می‌توانند مقدار بیشتری را نیز انتخاب کنند. برای نمونه می‌توان سطح توان آزمون را ۰/۹ درنظر گرفت یعنی به احتمال ۹۰% پژوهشگر از خطای نوع دوم اجتناب خواهد کرد. البته از مسائل بسیار مهم در تعیین توان آزمون سطح معناداری مورد انتظار است. بهتر است سطح خطا به صورت ۵% در نظر گرفته شود.

سخن پایانی

بیشتر آزمون‌های آماری استاندارد، دارای حداکثر توان آزمون هستند یعنی با فرض ثابت بودن خطای نوع اول در سطح ۵٪، خطای نوع دوم آن‌ها از هر آزمون دیگری کمتر است. در چنین حالتی احتمال خطای نوع اول را α و احتمال خطای نوع دوم را β می‌نامند. توان آزمون نیز به صورت ۱−β قابل محاسبه است که همان احتمال رد فرض صفر به حق است. به بیان دیگر توان آزمون نشان می‌دهد با چه احتمالی، تصمیم درست در رد فرض صفر اتخاذ شده است.

پس از آشنایی با آلفا و بتا، احتمالاً متوجه توازنی که بین آن‌ها وجود دارد شده‌اید. اگر بخواهید از مثبت‌های کاذب یا خطای نوع I اجتناب کنید، باید سطح اطمینان را بالا ببرید. اما هرچه در پرهیز از مثبت‌های کاذب مصرتر باشید، احتمال ایجاد منفی‌های کاذب یا خطای نوع دوم را افزایش می‌دهید.