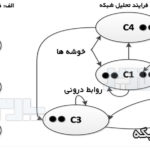
فرایند تحلیل سلسلهمراتبی فازی (FAHP)

روش فرایند تحلیل سلسلهمراتبی فازی (FAHP) روشی برای تحلیل ماتریس مقایسه زوجی با استفاده از منطق فازی میباشد. در روش مرسوم فرایند تحلیل سلسلهمراتبی از شایستگیها و تواناییهای ذهنی افراد خبره برای انجام مقایسات استفاده میشود. اما باید به این نکته توجه داشت که مقاسه زوجی به روش سنتی، امکان انعکاس سبک تفکر انسانی را بطور کامل ندارد. استفاده از اعداد فازی سازگاری بیشتری با عبارات کلامی و گاه مبهم انسانی دارد بنابراین بهتر است که با بکارگیری اعداد فازی به تصمیمگیری در دنیای واقعی پرداخت.
دو پژوهشگر هلندی به نام فان لارهوفن و پدریک به سال ۱۹۸۳ برای نخستین بار روشی را برای فرآیند تحلیل سلسلهمراتبی فازی پیشنهاد نمودند. این روش با جایگزینی اعداد فازی مثلثی در ماتریس مقایسههای زوجی و برمبنای حداقل مجذورات لگاریتمی بنا نهاده شده است. پیچیدگی مراحل این روش باعث شده این روش چندان مورد استفاده قرار نگیرد.
پس از آن روشهای متعددی برای فرایند تحلیل سلسلهمراتبی فازی پیشنهاد شد. سینگیز کاهرامان یا با تلفظ فارسی «چنگیز قهرمان» در کتاب تصمیمگیری چندمعیاره فازی، انواع روشهای فرآیند تحلیل سلسلهمراتبی فازی را بیان کرده است. در کتاب حاضر با استناد به کاهرامان روش بوکلی و روش چانگ که بیشتر مورد استفاده قرار گرفته است، آموزش داده شده است.
روش میانگین هندسی بوکلی
نظر به نارسائیهای نخستین روش AHP فازی، بوکلی به سال ۱۹۸۵ روش جدیدی را برای فازی سازی تکنیک AHP گسترش داد. این روش به روش میانگین هندسی بوکلی موسوم است. بوکلی دو ایراد اساسی به تکنیک لارهورن و پدریک وارد کرده است. نخست اینکه آنها از معادلات خطی استفاده کرده بودند و این روش ممکن است همیشه پاسخ یکسانی نداشته باشد. دوم اینکه اعداد ذوزنقهای برای فازیسازی دیدگاه خبرگان مناسبتر از از اعداد مثلثی است. بوکلی به سال ۲۰۰۱ اشاره کرده است که اگر سازگاری مقایسههای زوجی کامل باشد، در اینصورت نتیجه حاصل از روش وی با روش بردارویژه ساعتی یکسان خواهد بود در غیراینصورت نتایج روش وی بیشتر با واقعیت سازگار خواهد بود. ادامه مطلب …
روش بسط توسعه یافته چانگ
در سال ۱۹۹۲ روشی با عنوان روش تحلیل توسعهای توسط چانگ ارایه گردید. بعدها به سال ۱۹۹۶ این روش توسط خود وی بهبود بخشیده شد. روش گسترش یافته چانگ بیش از همه روشهای دیگر برای محاسبات تحلیل سلسهمراتبی فازی مورد استفاده قرار گرفته است. اعداد مورد استفاده در این روش، اعداد مثلثی فازی هستند. چانگ جهت تعمیم تکنیک AHP به فضای فازی از مفهوم درجه امکانپذیری استفاده کرده است. منظور از درجه امکانپذیری آن است که مشخص شود چقدر احتمال دارد یک عدد فازی بزرگتر از یک عدد فازی دیگر باشد. پیش از بیان الگوریتم پیشنهادی چانگ باید مفهوم درجه امکانپذیری یا درجه احتمال بزرگتر بودن تشریح شود. ادامه مطلب …
الگوریتم بهبود یافته فرایند تحلیل سلسلهمراتبی فازی
نخست با انتخاب طیف فازی مورد نظر، دادههای گردآوری شده در ماتریس مقایسه زوجی وارد میشود.

اگر بیش از یک کارشناس وجود دارد از میانگین هندسی فازی برای تجمیع دیدگاه خبرگان استفاده شود.
بسط فازی هر سطر
برای تعیین وزن اولیه هر عنصر از مفهوم بسط فازی استفاده میشود. چانگ برای بسط فازی عناصر هر سطر پیشنهاد کرده است که جمع اعداد فازی هر سطر حساب شود. اما بهتر است مطابق نظر بوکلی برای بسط فازی عنصر هر سطر از میانگین هندسی هر سطر استفاده شود.
بنابراین در ماتریس مقایسه زوجی فازی، میانگین هندسی عناصر هر سطر محاسبه میشود.
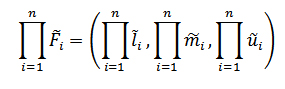
فرمول میانگین هندسی فازی
بسط فازی هر سطر وزن اولیه عنصر مندرج در آن سطر را نشان میدهد. این وزن باید نرمال شود.
چانگ برای نرمال سازی از مفهوم درجه امکان پذیری استفاده کرده است اما مطالعات متعدد نشان داده است این روش همیشه پاسخ صحیح بدست نمی دهد و ایرادات زیادی دارد. بنابراین از راهکار زیر استفاده کنید:
اگر میانگین هندسی هر سطر (بسط فازی هر سطر) را با Si نشان دهیم برای نرمال سازی جمع تمامی بسط فازی همه سطرها (وزنهای اولیه فازی) را حساب کنید. مجموع ترجیحات تمامی عناصر یعنی Σ(Si) محاسبه میشود.
برای نرمالسازی باید بسط فازی هر عنصر Si بر مجموع تمامی ترجیحات Σ(Si) تقسیم شود. چون مقادیر فازی هستند از فرمول زیر برای محاسبه وزن هر عنصر استفاده میشود:
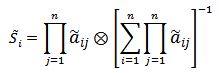
نرمال سازی وزن در AHP فازی
وزن محاسبه شده، وزن نهایی عنصر مورد بررسی است. این اوزان فازی است برای محاسبه وزن قطعی از روش فازی زادیی استفاده کنید. انواع روش های فازیزدایی را میتوانید برای این منظور استفاده کنید. این مرحله گام مهمی در فرایند تحلیل سلسلهمراتبی فازی است.
اوزان قطعی بدست آمده را به روش نرمالسازی خطی، نرمال کنید.
منبع: حبیبی، آرش؛ آفریدی، صنم. (۱۴۰۱). تصمیمگیری چندشاخصه، تهران: انتشارات نارون.
تصمیم گیری چندمعیاره | ۲۹ بهمن ۹۳