مدل معادلات ساختاری
مدل معادلات ساختاری روشی برای بررسی روابط میان متغیرهای پنهان است که همزمان متغیرهای مشاهدهپذیر را نیز در نظر میگیرد. منظور از متغیرهای پنهان همان عوامل اصلی هستند که در یک الگو یا مدل مفهومی نمایش داده میشوند. متغیرهای مشاهدهپذیر نیز همان گویهها یا سوالات مربوط به سنجش عوامل اصلی میباشند.
«مدلیابی معادلات ساختاری» برگردان Structural Equation Model است که به اختصار SEM نیز نامیده میشود. این روش یک ساختار علی ویژه بین مجموعهای از متغیرهای پنهان و متغیرهای مشاهدهپذیر است. با استفاده از روش مدلیابی معادلات ساختاری روابط بین متغیرهای پنهان با یکدیگر و نیز گویههای سنجش هر متغیر پنهان با متغیر مربوط قابل بررسی است. برای انجام محاسبات این روش از نرمافزار لیزرل یا نرمافزار اموس استفاده میشود.
روش مدلیابی معادلات ساختاری آن است که این روش برای ساخت مدل استفاده نمیشود بلکه برای ارزیابی و اعتبارسنجی مدل کاربرد دارد. در واقع پژوهشگر باید یک مدل اولیه را ترسیم کند سپس با استفاده از این روش به اعتبارسنجی مدل بپردازد. نظر به کاربرد وسیع این روش در مدیریت و علوم اجتماعی در این مقاله به تشریح کامل مدل معادلات ساختاری پرداخته شده است.
پیدایش مدل معادلات ساختاری
یکی از موضوعات اصلی پژوهشهای مدیریت بررسی روابط بین عناصر بوده است. نخستین بار کارل پیرسون با ارائه روش همبستگی کوشش کرد تا روشی آماری برای بررسی روابط بین عناصر ارائه نماید. روش همبستگی پیرسون با وجود مزایایی که داشت اما روابط متغیرها را همواره دو به دو بررسی میکرد. در این روش نقش متغیرهای دیگر مدل در روابط میان سایر عناصر در نظر گرفته نمیشود. مدلهای نظری چند متغیره را نمیتوان با شیوه دو متغیری که هر بار تنها رابطه یک متغیر مستقل با یک متغیر وابسته در نظر گرفته میشود، ارزیابی کرد.
برای رفع این مشکل روش رگرسیون مطرح گردید. در روشهای رگرسیونی بر خلاف روشهای همبستگی نقش عناصر مختلف در رابطه عوامل موجود در مدل در نظر گرفته میشود. برای درک بهتر موضوع مقاله تفاوت رگرسیون و همبستگی را مطالعه کنید. اما نقطه ضعف اصلی روش رگرسیون و تحلیل مسیر نیز در عدم امکان در نظر گرفتن همزمان همه گویههای شکل دهنده متغیرهای اصلی بوده است. برای رفع این مشکل مدل معادلات ساختاری طراحی شد.
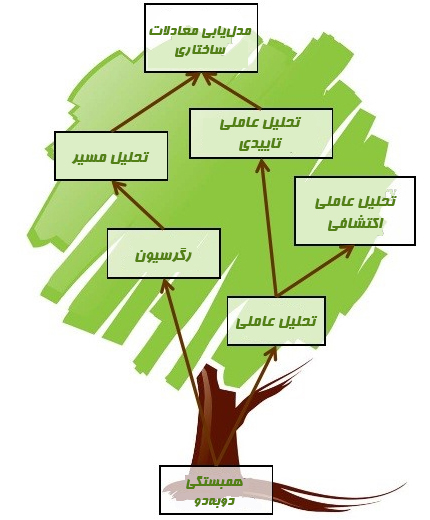
پیدایش و فرگشت مدل معادلات ساختاری
مدل معادلات ساختاری یکی از انواع تحلیلهای همبستگی است که در دسته تحلیل ماتریس کوواریانس یا ماتریس همبستگی قرار میگیرد. تحلیل ماتریس کووایانس با توجه به هدف و نوع تحلیل به دو دسته اصلی تحلیل عاملی و مدلهای ساختاری تقسیم میشود:
- تحلیل عاملی Factor Analysis
- مدل معادلات ساختاری Structural equation model, SEM
هر دو این تحلیلها از طریق نرمافزار لیزرل و اموس قابل انجام است.
روش انجام مدل معادلات ساختاری
مدل معادلات ساختاری یا Structural Equation Model یک ساختار علی خاص بین مجموعهای از سازههای غیرقابل مشاهده است. یک مدل معادلات ساختاری از دو مولفه تشکیل شده است: یک مدل ساختاری که ساختار علی بین متغیرهای پنهان را مشخص میکند و یک مدل اندازهگیری که روابطی بین متغیرهای پنهان و متغیرهای مشاهده شده را تعریف میکند.
گامهای انجام تحقیق با تکنیک مدلیابی معادلات ساختاری عبارتند از:
- شناسایی متغیرهای اصلی تحقیق
- تهیه پرسشنامه برای سنجش متغیرها : تعیین گویههای سنجش هر متغیر اصلی
- تدوین فرضیههای تحقیق: تعیین روابط میان متغیرهای اصلی مدل
- طراحی مدل مفهومی براساس فرضیههای تحقیق
- توزیع پرسشنامهها و گردآوری دادهها
- طراحی مدل ساختاری و اجرای مدل با نرمافزار لیزرل یا اموس
متغیر پنهان و متغیر قابل مشاهده
سازهها یا متغیرهای پنهان و آشکار دو مفهوم اساسی در تحلیلهای آماری بویژه بحث تحلیل عاملی و مدلیابی معدلات ساختاری هستند.
متغیرهای پنهان Latent Variables که از آنها تحت عنوان متغیر مکنون نیز یاد میشود متغیرهائی هستند که به صورت مستقیم قابل مشاهده نیستند. برای مثال متغیر انگیزه را در نظر بگیرید. انگیزه فرد را نمیتوان به صورت مستقیم مشاهده کرد و سنجید. به همین منظور برای سنجش متغیرهای پنهان از سنجهها یا گویههائی استفاده میکنند که همان سوالات پرسشنامه را تشکیل میدهند. این سنجهها متغیرهای مشاهده شده هستند.
متغیرهای مشاهده پذیر Observed variables گویهها یا سنجههایی هستند که برای اندازهگیری متغیرهای پنهان استفاده میشوند. برای مثال سختکوشی، حضور بهموقع در محل کار، حساسیت به انجام کار و مواردی از این دست متغیرهای قابل مشاهده برای متغیر پنهان انگیزش هستند.
طراحی یک مدل معادلات ساختاری
طراحی یک مدل معادلات ساختاری با ذکر یک مثال توضیح داده میشود. برای نمونه در پژوهشی رابطه سه متغیر پنهان A,B,C بررسی میشود. رابطه علی بین این متغیرها به این صورت در نظر گرفته شده است:
۱- متغیر پنهان A یک متغیر مستقل است و بر هر دو متغیر پنهان B و C تاثیر دارد.
۲- برای سنجش متغیر پنهان A از دو متغیر قابل مشاهده A1 و A2 استفاده شده است.
۳- برای سنجش متغیر پنهان B از دو متغیر قابل مشاهده B1 و B2 استفاده شده است.
۴- برای سنجش متغیر پنهان C از سه متغیر قابل مشاهده C1 و C2 و C3 استفاده شده است.
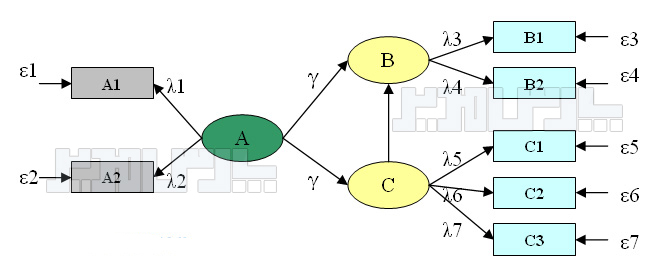
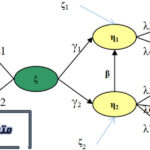
ساختار کلی مدل معادلات ساختاری؛ منبع: حبیبی، ۱۳۹۵ ص ۱۰
مدل کلی معدلات ساختاری از الگوی شکل ۲-۳ پیروی میکند. قوانین این الگو عبارتند از:
۱- هر بیضی در مدل معادلات ساختاری نشاندهنده یک متغیر پنهان است.
۲- هر مستطیل در مدل معادلات ساختاری نشاندهنده یک متغیر قابل مشاهده است.
۳- از هر متغیر پنهان(بیضی) به هر متغیرقابل مشاهده(مستطیل) پیکانی وجود دارد که با نماد λ نشان داده میشود. به λ وزنهای عاملی یا بار عاملی گفته میشود. طبق گفته کلاین بارهای عاملی بزرگتر از ۰.۳ نشاندهنده با اهمیت بودن رابطه است.
۴- هر مقدار ε نیز نشاندهنده خطا در پیشبینی متغیرهای پنهان از یکدیگر است.
۵- ضریب رابطه علی بین دو متغیر پنهان مستقل و وابسته با γ نشان داده میشود.
۶- ضریب رابطه علی بین دو متغیر پنهان وابسته با β نشان داده میشود.
بار عاملی (Factor Loading)
قدرت رابطه بین عامل (متغیر پنهان) و متغیر قابل مشاهده بوسیله بار عاملی نشان داده میشود. بار عاملی مقداری بین صفر و یک است. اگر بار عاملی کمتر از ۰.۳ باشد رابطه ضعیف درنظر گرفته شده و از آن صرفنظر میشود. بارعاملی بین ۰.۳ تا ۰.۶ قابل قبول است و اگر بزرگتر از ۰.۶ باشد خیلی مطلوب است. (کلاین، ۱۹۹۴)
بار عاملی در شکل با λ نشان داده شده است. در تحلیل عاملی متغیرهائی که یک متغیر پنهان (عامل) را میسنجند، باید با آن عامل، بار عاملی بالا و با سایر عاملها، بار عاملی پائین داشته باشند. در نرمافزار لیزرل بار عاملی از طریق گزینه Standardized solution از لیست Stimates محاسبه میشود.
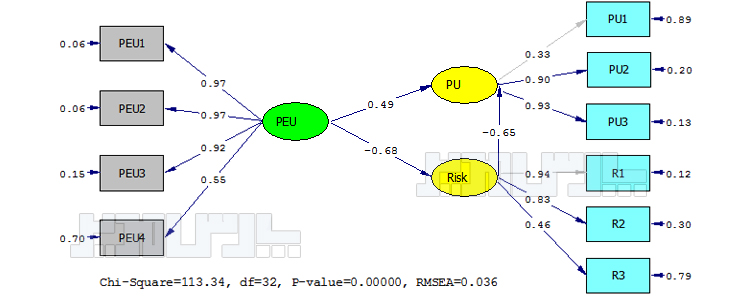
جهت بررسی معنادار بودن رابطه بین متغیرها از آماره آزمون t یا همان t-value استفاده میشود. چون معناداری در سطح خطای ۰.۰۵ بررسی میشود بنابراین اگر میزان بارهای عاملی مشاهده شده با آزمون t-value از ۱.۹۶ کوچکتر محاسبه شود، رابطه معنادار نیست و در نرمافزار لیزرل با رنگ قرمز نمایش داده خواهد شد.
خلاصه و جمعبندی
مدلیابی معادلات ساختاری یک روش آماری برای اعتبارسنجی مدل مفهومی پژوهش است. پژوهشگر ابتدا باید عوامل مختلف شکلدهنده پدیده مورد بررسی را شناسایی کند. سپس براساس مبانی نظری موجود روابط بین عوامل را حدس بزند و فرضیهسازی کند. همچنین برای هر عامل باید تعدادی گویه جهت سنجش شناسایی کند. پس از فرضیهسازی و ترسیم مدل مفهومی اولیه، این مدل باید در محیط نرمافزار اموس یا لیزرل پیادهسازی شود. در نهایت با استفاده از روش مدل معادلات ساختاری میتوان مدل مفهومی را اعتبارسنجی کرد.
منبع: حبیبی، آرش؛ کلاهی، بهاره. (۱۴۰۱). مدلیابی معادلات ساختاری و تحلیل عاملی. تهران: جهاد دانشگاهی، چاپ دوم.
آمار کاربردی مدیریت | ۱۴ فروردین ۹۶



سلام وسپاس فراوان از مطلب خوبتون
ببخشید میشه منبع مطلب بالا رو بصورت دقیق ذکر کنید تا در پایان نامم بذارم؟؟؟؟
و منبع کلاین ۱۹۹۴ رو که در متن بالا هست. سپاس از لطفتون
حبیبی، آرش؛ کلاهی، مریم. (۱۳۹۶)، مدلیابی معادلات ساختاری و تحلیل عاملی، تهران: انتشارات جهاد دانشگاهی، ویرایش ششم.
Kline, Rex. (2011), Principles and Practice of Structural Equation Modeling (Methodology in the Social Sciences), New York: Guilford Press, 3rd Edition. ISBN-13: 978-1606238769.
لطفا بفرمایید مدل یابی معادلات ساختاری به صورت کوتاه، سریع و کاربردی چیست و چگونه انجام میشود؟
مدل یابی معادلات ساختار تکنیک خوبی است و با نرم افزار لیزرل انجام میشود.
سلام. آیا مدل های رگرسیونی زیر مجموعه ای از SEM هستند یا در دسته جداگانه ای قرار میگیرند؟؟
در واقع مدلهای ساختاری زیرمجموعه روشهای رگرسیونی هستند.
با سلام
فرق روش ism با sem در چیست؟؟
روش مدلسازی ساختاری-تفسیری همونطور که از اسمش پیداست برای مدلسازی هست و جنبه اکتشافی داره، یعنی شما یک دسته متغیر دارید میخواهید الگوی روابط متغیرها رو پیدا کنید.
مدل معادلات ساختاری جنبه تاییدی داره، یعنی شما یک مدل دارید و میخواهید اعتبار مدل رو مورد سنجش قرار بدید.
تعریف مرحله اول انعکاسی و دوم ترکیبی در تحلیل آماری چیست ؟
با سلام و تشکر از مطالب بسیار غنی که تو سایت بارگذاری میشه.
سوال من اینه که ( پیش بینی قدرت مدل ) یعنی چه؟ و به وسیله (چه شاخصهایی) سنجیده میشه؟
منظور از قدرت پیش بینی مدل توانایی مدل در برآورد متغیرهای وابسته (ملاک) با توجه به متغیرهای مستقل (پیشبین) است. بارعاملی و ضریب تعیین مهمترین شاخصها در این زمینه هستند.
جناب حبیبی براتون امکان داره راجع به(براورد متغیرهای وابسته)که تو فرمایشتون بود، توضیح بیشتری بدید؟
منظور همون بارهای عاملی هست و مقدار ضریب تشخیص، در متن آموزش توضیحات بیشتری نوشته شده.
با سلام و عرض خسته نباشید
ابتدا” از سایت عالیتون و مطالبی که منتشر می فرمایید تشکر می کنم.
می خواستم بدونم ترتیب ارائه فرضیه بعد از مدلسازی ساختاری تفسیری به چه صورته؟ آیا بعد از رسیدن به مدلism با توجه به مدلT فرضیه ها رو ارائه می دیم و بعد با مدل سازی معادلات ساختاری فرضیه ها رو آزمون می کنیم؟ یا بعد از محاسبات sem?
بعد از مدلسازی ساختاری-تفسیری یک الگوی اولیه بدست میاد که براساس روابط موجود میتونید فرضیهسازی کنید و بعد با مدلیابی معادلات ساختاری به آزمون فرضیهها بپردازید.
سلام
معادلات ساختاری جز روش های تحقیق است؟ یعنی جز روش های تحقیق کمی حساب می شود؟
نکته بسیار مهم: روش تحلیل با روش تحقیق تفاوت دارد. روش تحقیق براساس هدف و شیوه گردآوری دادهها دستهبندی میشه و روش تحلیل شامل فنونی برای حل مساله و پاسخ به سوالات یا آزمون فرضیهها است. مدل ساختاری یک روش تحلیل داده است.
با سلام
سوال من اینه اگه عنوان کار ارائه مدل باشه
میتونیم فقط از معادلات ساختاری استفاده کنیم؟
یا باید اول از معادلات تفسیری مدل بسازیم بعد با ساختاری تایید کنیم
حتما باید از یک راهی الگوی اولیه را بسازیم. دیمتل و ای اس ام دو نمونه روش برای طراحی الگو هستند و ممکن است بتوانید براساس ادبیات پژوهش فرضیهپردازی کنید.
سلام و احترام
ممنون از مطالب خوبتون
آیا در معادلات ساختاری تعریف متغیر مستقل و وابسته قبل از اجرای مدل کار درستی است؟ چون نتیجه گاهی اواقت ارتباط دوسویه میان متغیر ها را نشان می دهد و جای متغیر وابسته و مستقل تغییر می کند
در مدلسازی معادلات ساختاری باید روابط از قبل مشخص باشد. همینطور رابطه دوسویه نداریم.
سلام و عرض ادب ممنون از مطالب مفیدتون.معادلات ساختاری را میتوان در دو گروه بکار برد .متغیر مستقل و وابسته و میانجی داریم در دو قومیت
درود بر شما. برای این منظور بهتر هست قومیت را به عنوان متغیر تعدیلگر درنظر بگیرید و مساله را روش حداقل مربعات جزئی یا رگرسیون سلسلهمراتبی حل کنید. متاسفانه راهکار مستقیم برای متغیرهای تعدیلگر در نرم افزار لیزرل نمیشناسم.
سلام. وقتبخیر. اگر تمام مراحل گفته شده انجام بشه فقط برای تحلیل از نرمافزار plsاستفاده کنیم به خاطر کم بودن تعداد نمونه، نتایج نامعتبر میشه، جایی خوندم در روش حداقل مربعات جزیی برای مطالعات فرضیهای کاربرد نداره ممنون میشم نظرتون رو بفرمایین
درود بر شما. شخصاً تابحال در منبع معتبری ندیدم که صراحتاً بیان شده باشه حداقل مربعات جزئی فاقد اعتبار هست یا برای آزمون فرضیه کاربرد نداره.
با سلام
میخواستم بدونم برای استفاده از مدل یابی معادلات ساختاری الزاما همه متغیرهای آشکار باید دارای مولفه های پنهان باشند؟ یا اینکه میشود یکی از متغیرهای آشکار فقط متغیر پنهان داشته باشد یکی نداشته باشد؟
درود. شما نیاز اکید دارید تا با مطالعه متغیر پنهان و آشکار با این مفاهیم به صورت زیربنایی آشنا شوید.
با سلام و وقت بخیر
از مطالب و توضیحات مفید و کاربردی مدل معادلات ساختاری سپاسگذاریم.
یک سوال خدمت جنابعالی داشتم ممنون میشم راهنمایی کنید
آیا برای کار پژوهشی شناسایی چالشها و مشکلات تجارت بین دو منطقه(نه کشور) که از طریق مصاحبه و پرسشنامه انجام شود برای روش شناسی، روش سوات مناسب تر است یا مدل معادلات ساختاری؟
درود بر شما. بدون تردید تحلیل استراتژیک مانند سوات، ماتریس بررسی رقابت، ماتریس برنامهریزی کمی و ….
باسلام و تشکر از سایت مفید و کاربردی تون،
ببخشید در خصوص تحلیل داده ها در معادلات ساختاری، وقتی میگوییم ضریب مسیر بین دو متغیر مثبت است یعنی اثر مستقیم دارن؟ و اینکه بر اساس آماره t معنادار شده یعنی ارتباط وجود دارد؟ و هردو رو در تحلیل مورد بررسی قرار میدهیم؟ هردو ملاک بررسی قرار میگیره؟
درود بر شما. بارعاملی جهت و شدت رابطه را نشان میدهد آماره تی هم معنادار بودن. اگر بارعاملی مثبت باشد رابطه مستقیم و اگر منفی باشد رابطه معکوس است.
سلام و عرض ادب
وقت بخیر
در روش حداقل مربعات جزئی، هم ضرایب بارهای عاملی رو داریم که به فرموده شما، شدت رابطه رو نشون میده، و هم F2 (کوهن ۱۹۸۸) رو داریم که اون هم شدت اثر رو نشون میده.
فرق اینا چیه و من برای نتیجهگیری از کدوم باید استفاده کنم؟
درود بر شما. ضریب مسیر جهت و شدت تاثیر یک متغیر مستقل بر یک متغیر وابسته را نشان میدهد. اگر همزمان چند متغیر بر یک متغیر وابسته اثر بگذارند با استفاده از اندازه اثر مشخص میشود در صورت نبود یک متغیر مستقل چه تغییراتی را در پیش بینی متغیر وابسته رخ میدهد.
با سلام ممنون مطالب مفید سایتتون.
وققتون روش کار سرشماری می باشد می شود برلی بررسی فرضیات از معادلات ساختاری استفاده کرد یا فقط با امار توضیفی و همبستگی گزارش بدیم
درود بر شما. روش نمونهگیری ارتباطی با روش تحلیل دادهها ندارد. البته محاسبه حجم نمونه به روش تحلیل دادهها بستگی دارد.
با سلام، در مدل معادلات ساختاری می توان رابطه بین متغیرهای مشاهده پذیر دو متغیر پنهان را با یکدیگر بررسی کرد؟ به عبارت دیگر در مثال بالا مثلا می توارابطه بین A1 را با B1 سنجید؟ با تشکر
درود بر شما. خیر، فقط روابط متغیرهای پنهان بررسی میشود.
با درود و سپاس از سایت خوب و مطالب کاربردیتون .
میشه خواهش کنم راهنمایی بفرمایید که چگونه می شودبهتر و ساده تر با مفاهیم و موضوعات مرتبط با مبحث مدلسازی معدلات ساختاری، متغیر پنهان،آشکارو… به صورت زیربنایی آشنا شد؟
درود بر شما. آموزشها و ویدیوهای سایت را به دقت مطالعه کنید.
درود بر شما . سوالی داشتم ، با توجه به پاسخی که به یکی از پژوهشگر های این سایت داده بودید ؛
(مدل یابی معادلات ساختار تکنیک خوبی است و با نرم افزار لیزرل انجام میشود) آیاهمیشه باید با نرم افزار لیزرل انجام شود ؟ با PLS چطور ؟می شود ؟
مدل معادلات ساختاری با نرمافزار لیزرل و اموس قابل انجام است. روش حداقل مربعات جزئی مبتنی بر مدل معادلات ساختاری ایجاد شده و یک روش ناپارامتریک است. از نظر آماری روش SEM نسبت به PLS-SEM آزمون سطح بالاتری محسوب میشود.
ممنون از شما
سلام
مدلی که من دارم دارای ۳ متغیر پنهان و جمعا ۱۳ متغیر آشکار در حوزه روانشناسی هست. برای راهنمایی جهت طرح سوالات تحقیق و مراحل تحلیل داده ها شدیدا نیازمند یک منبع قابل دسترس و با پرداحت هزینه هستم. متاسفانه در شرایط مجازی اساتیدم جوابگو نیستن و الگوگیری از مقالات مشابه کارساز نبوده چون استادم گفتن اشتباهه ولی پاسخگوی سوالاتم نبودن
درود بر شما. با شمارههای پشتیبانی سایت تماس بگیرید.
با سلام، در این روش حتما باید فرضیه هم داشته باشیم یا داشتن متغیرهای مستقل و وابسته کافیه؟
خواه از عنوان فرضیه استفاده کرده باشید خواه اسمی از فرضیه نبرده باشید وقتی متغیری رو به عنوان مستقل در نظر میگیرد و متغیری رو به عنوان وابسته در واقع در مورد رابطه این دو متغیر فرضیهسازی کردید.
سلام
در روش معادلات ساختاری با رویکرد پی ال اس باید حتما داده ها از پرسشنامه باشه یا منی که دادهام از صورتهای مالی هم هست میتونم استفاده کنم؟
و
درود بر شما. دادههای مالی از نوع نسبی است و ارزش عددی بسیار بهتری دارد. این نوع مقادیر برای محاسبات رگرسیونی (رگرسیون، مدل ساختاری و حداقل مربعات جزئی) بهتر است.
سلامو سپاس از مطالب مفیدتون
آیا در معادلات ساختاری متغیر مستقل می تواند اسمی باشد
درود بر شما. استفاده از متغیرهای اسمی-ترتیبی در مدلهای معادلات ساختاری صحیح نیست. مقیاس متغیرها باید نسبی-فاصلهای باشد.
سلام ایا امکان انجام مدل اماری از جانب شنا هست؟
سلام و خداقوت بابت سایت عالی. چند ساعت نشستم و مطالب مختلف رو مطالعه کردم.
روش های آزمون مدل سنجش test model measurement و آزمون مدل ساختاری model structural test در پژوهش کمی، همین مبحثه یا متفاوته؟
درود بر شما. بله به ترتیب به مدل اندازه گیری و بخش ساختاری مدل اشاره دارند.
سپاسگزارم. الان که برای دیدن صفحه مراجعه کردم و پاسخ زود هنگامتون رو دیدم خیلی خوشحال شدم.
الان که سوال منتشر شده م رو دیدم، متوجه شدم ترتیب کلمات در عبارات انگلیسی به هم ریخته. برای مخاطبینی که مثل من برای آموزش بیشتر به کامنتها مراجعه می کنند:
Measurement Model test
Structural Model test
یک مدل معادلات ساختاری دو بخش اصلی دارد:
مدل اندازهگیری (Measurement Model) که رابطه متغیرهای پنهان و مشاهدهپذیر را نشان میدهد.
مدل ساختاری (Structural Model) که رابطه متغیرهای پنهان را نشان میدهد.
سلام به آقای حبیبی و تیم پارس مدیر خسته نباشید و ممنون بابت مطالب
سوالی داشتم از خدمتتون
جنسیت، شغل و تحصیلات سه تا از متغیرهای مشاهده پذیر من هستند آیا میتونم از مدل معادلات ساختاری استفاده کنم ؟
درود بر شما. این متغیرها اسمی هستند و ارزش عددی ندارند بنابراین استفاده از آنها در مدلهای ساختاری به شدت مورد تردید است.
ممنون از پاسخ حضرتعالی.
سلام . از معادلات ساختاری میشه برای داده های مالی استفاده کرد؟دادهای من از طریق پرسشنامه جمع اوری نشده
درود بر شما. بله، مقادیر مالی از نوع نسبی هستند و از دادههای پرسشنامه طیف لیکرت، ارزش عددی بهتری دارند.
سلام ممنون از مطالب خوبتون
تعریف عملیاتی مدل یابی معادلات ساختاری چیست؟
باتشکر
درود بر شما. روش آماری تعریف عملیاتی ندارد. آموزش تعریف مفهومی و عملیاتی را مطالعه کنید.
سلام در تحقیقی متغیر مستقل کم آبی است با دوبعد کم آبی سطحی وکم آبی زیرزمینی و متغیر وابسته احساس امنیت اجتماعی است با چهاربعد شامل امنیت مادی، امنیت جانی، امنیت جمعی وامنیت فکری برای ساخت مدل چه کنم؟
درود و خدا قوت به جناب حبیبی؛ سپاس از مطالب خوب و ارزشمند تون و حسن پاسخگویی به پرسشگران و نشر علم
درود بر شما. ارادتمندم
با سلام واحترام در نظر دارم رساله خود را در مقطع دکتری به توسط مالتی گرندد تئوری اغاز نموده وپس از رسیدن به مدل یا الگو از طریق sem یا معادلات ساختاری ازمون کنم نظر شما چیست؟
درود بر شما. ایده خوبی است البته روش مولتای گراندد هنوز به اندازه کافی تئوریزه نشده و مبانی نظری و درک کافی از این روش وجود ندارد.
با سلام. آیا پرسشنامه هایی به تعداد جامعه آماری ۱۰ تا ۲۰ نفره در مدل معادلات ساختاری جوابگو هست؟ حداقل و حداکثر جامعه آماری برای جوبگو بودن با SmartPls چند نفر هست؟
درود بر شما. آموزش تعیین حجم نمونه و تعیین حجم نمونه PLS را مطالعه کنید.
سلام.موضوع من در مورد “تاثیر مدیریت هزینه بررقابت بازار محصول با تاکید بر نقش تعدیلگر تمرکز مشتری و مشکل نمایندگی” است.البته مدل رگرسیونی هم دارم.میخواستم بدونم امکان استفاده از مدل ساختاری وجود داره?
درود بر شما. نرمافزار لیزرل راهکار مستقیمی برای محاسبه اثر تعدیلگری متغیرها ندارد. از رگرسیون یا حداقل مربعات جزئی استفاده کنید.
سلام مجدد. من مقالهای دیدم که متغیر تعدیگر دارد و برای تحلیل دادهها هم از نرمافزار اسمارت پی ال اس و از روش حداقل مربعات جزئی استفاده کردهاند.
باسلام. ممنون از مطالب مفید سایت شما. در برازش مدل در نرم افزار آموس و لیزرل آیا نیاز هست تمامی شاخص های برازش بالای ۰/۹ باشند اگر دو تا مثلا ۰/۸۵ بود برازش درست است. با تشکر
درود بر شما. عرف این است که ۵ تا ۸ شاخص را گزارش میکنند یکی دو شاخص متفاوت باشد قابل اغماض است.
سلام.بجزمعادلات ساختاری از چه روشهای دیگری برای تحلیل مدل کمی میشه استفاده کرد؟چه معیاری باعث میشه که تحلیل کواریانس یا واریانس انتخاب بشه؟روش رگرسیون که درspss استفاده میشه متفاوت ازمعادلات ساختاریه؟
درود بر شما. برای اعتبارسنجی و برازش مدل سه راهکار دارید: رگرسیون و تحلیل مسیر؛ حداقل مربعات جزئی و مدل معادلات ساختاری
رگرسیون مبنای زیربنایی مدلهای معادلات ساختاری است اما نمیتواند همزمان مدل اندازهگیری را در نظر بگیرد و فقط روی بخش ساختاری مدل متمرکز است.
سلام جناب حبیبی عزیز
پنج تا متغیر روان شناسی با حجم نمونه ۵۰۰تایی دارم و می خوام یه مدل معادلات ساختاری رو در موردشون بررسی کنم استفاده از کدوم برنامه رو توصیه می کنید؟
سپاس
درود بر شما. با حجم نمونهای که دارید و تعداد متغیرهای معقولی که وجود دارد از لیزرل یا اموس استفاده کنید بهتر است. این دو نرمافزار از نظر آماری برتری ویژهای نسبت به هم ندارند و سلیقهای است شخصا لیزرل را ترجیح میدهم. اگر تعداد سوالات سنجش متغیرها بیش از ۳۰ یا ۴۰ گویه باشد یا متغیر تعدیلگر داشته باشید مجبور هستید از لیزرل صرفنظر کنید.
سلام و وقتتون بخیر ببخشید یه سوال داشتم پژوهش هایی که عنوانش با روابط ساختاریبن چند متغیر شروع میشه برای تحلیل فقط میتونن از روش معادلات ساختاری استفاده کنن یا روش تحلیل مسیر هم میشه؟
سلام وقت بخیر با سپاس از سایت عالی و پر بار تون ، ممکنه راجع به انواع مدل توضیح بدید ، منظورم زیر مانند و همانند و زبر مانند هست و اگریکی از مسیر های مدل حذف گردد در چه صورت زیر مانند میشود،
درود بر شما. این اصطلاحات را برای نخستین بار هست میشنوم. معادل لاتین را ذکر کنید.
سلام سوالی داشتم اگر تعداد سوالات متعیر ها زیاد باشه معالات ساختاری رو نمیشه اجرا کرد؟؟
درود بر شما. بیش از ۳۰ تا ۴۰ سوال کلا صحیح نیست. ضمن اینکه لیزرل به ندرت با بیش از این تعداد ران میشود.
سلام و سپاس از مطالب خوبتون.
پس از اجرا و برازش کلی مدل (انعکاسی) در PLS، آیا درسته که شاخص ها رو بر اساس بارعاملی اولویتبندی کنیم؟ آیا در مدل انعکاسی یافته ای داریم که وزن شاخص رو به ما نشون بده؟
درود بر شما. ضریب مسیر و اندازه اثر شاخص مناسبی برای قضاوت پیرامون میزان اثرگذاری یک دسته سازه بر یک سازه مشخص است.
سلام، ممنون از اطلاعاتی که گذاشتید. میخواستم بپرسم که برای انجام روش معادلات ساختاری حتما باید اول آنالیز فاکتور یا تحلیل عاملی انجام دهیم
درود بر شما. خیر، ولی براساس یک عرف اشتباه در نظام آموزش عالی کشور این کار انجام میشود.
ممنون، آیا متغیرهای آشکار و پنهان را خودمان باید مشخص کنیم
بله، آموزش متغیر پنهان و مشاهدهپذیر را مطالعه کنید.
هم مقاله و توضیحات بسیار عالی و گویا بیان شده و هم در پاسخ به سوالات دوستان ، بزرگواری و سواد جنابعالی مشهود هست. به عنوان یک علم آموز از شما عمیقاً سپاسگزارم 🌺🙏
ارادتمندم
ممنون کتابتون رو میخواستم؟
باسلام ممنون ازمطلب خوبتون بنده پایان نامه ام معادلات ساختاری است وتحلیل گرآماری اماری بنده ازبرنامهpls استفاده کرده می خواستم بدانم تفاوت بین لیزرل با اسمارت پی ال اس چیست؟
درود بر شما. لیزرل نرمافزاری برای انجام مدلیابی معادلات ساختاری مبتنی بر ماتریس کوواریانس (CB-SEM) است و اسمارت پیالاس نرمافزاری برای مدلیابی معادلات ساختاری مبتنی بر حداقل مربعات جزئی (PLS-SEM) است.
عالی بود .مرسی از سایت خوبتون
سلام وقت بخیر، تفاوت بین معادلات ساختاری، حداقل مربعات جزِئی و تحلیل عاملی در چیه؟
درود بر شما. تفاوت این دو رویکرد در آموزش مندرج در کتاب حداقل مربعات جزئی مطالعه کنید.
با سلام بنده برای پایان نامه ام از sem دارم استفاده میکنم ولی در چگونگی کشیدن مدل به مشکل برخوردم آیا امکانش هست لطف کنید کمکم کنید
عالی وسپاس
سلام و عرض ادب و احترام.
مطلب بسیار ساده ، روان و قابل فهم توضیح داده شده بود. دعای خیر بدرقه شما و تمامی معلمانی که بدون اغماض علم خویش را به دیگران می آموزند.
درود بر شما. 🌷🌷🌷